Operationsverstärker I

• Elektronik-Minikurse: Inhaltsverzeichnis   WICHTIG: Diverse technische Infos
• Elektronik-Minikurse: Philosophie (Sinn, Vorwissen, Praxisbezug)
• Hilfe bei Leserfragen. (WICHTIG: Unbedingt zur Kenntnis nehmen!)
• Simulieren und Experimentieren, ein Vorwort von Jochen Zilg
• Autor:   Thomas Schaerer      Opamp-Buch   Timer555-Buch

1.  Einleitung

Auf englisch heisst der Operationsverstärker Operational-Amplifier. Abgekürzt bezeichnet man ihn, auch im deutschsprachigen Raum, oft als Opamp. Ganz korrekt müsste man OpAmp schreiben, wobei man in der Fachliteratur sehr oft auch Opamp liest. In meinen Elektronik-Minikursen kommen immer wieder beide Begriffe, also Operationsverstärker und Opamp, vor. Opamps sind wesentlich komplexer als es beim Elektronik-Anfänger den Anschein erweckt. Dies kommt hier darin zum Ausdruck, dass ein Kapitel sich nicht nur gerade auf seinen Untertitel fixiert. So steht im folgenden Kapitel 2 das Thema der virtuellen Masse, bzw. virtuellen GND (Ground), auch in einem gewissen Zusammenhang mit der Geschwindigkeit des Opamp (Unity-Gain-Bandbreite).

Dieser erste Elektronik-Minikurs über Operationsverstärker (Opamps) befasst sich mit der invertierenden und nichtinvertierenden Verstärkung. Thematisiert wird der virtuelle GND, bzw. die virtuelle Spannung, und warum die Differenzspannung am Eingang im eingeschwungenen Zustand (fast) immer 0 V sein muss. Ebenfalls werden die DC-Offsetspannung und die Kompensationsmethoden, die Arbeitspunktspannung (Referenzspannung), wenn nur eine Betriebsspannung (Single-supply) zur Verfügung steht und die Geschwindigkeitsgrenzen des Operationsverstärkers thematisiert. Dabei wird ausführlich erklärt was die Unity-Gain-Bandbreite (UGBW) und die Slewrate ist und wie man damit, an einem praktischen Beispiel gezeigt, umgeht.

Es wird gezeigt, wie man eine einfache Messschaltung für Hochspannung realisieren kann. An anderer Stelle lernt man wie bei einer Schaltung zur Erzeugung einer aktiven Referenzspannung eine ungewollte störende parasitäre Induktivität entstehen kann, wenn man diese Schaltung nicht richtig dimensioniert, was allerdings keine schwierige Sache ist. Ein interessantes aber störendes Phänomen erzeugen (Multilayer-)Keramik-Kondensatoren (Kerko) als akustische Wandler (Piezoeffekt). Es geht darum, wie man dies durch vernünftige Dimensionierung von RC-Schaltungen vermeidet.

Neben den angedeuteten Spannungspunkten bzw. Spannungsknoten gibt es auch Strompunkte bzw. Stromknoten in Opamp-Schaltungen. Der wichtigste Stromknoten ist der invertierende Eingang, wenn der Opamp als Verstärker mit einer Gegenkopplung arbeitet. Dieser Stromknoten ist bekanntlich durch die Knotenregel, auch bekannt unter der Bezeichnung "Erste Kirchhoffsche Regel", definiert. Wie es zur virtuellen Spannung (virtueller GND) am invertierenden Eingang kommt, wird genau erklärt. Da scheint es in Bezug auf Strompfeilangaben, auch in der Fachliteratur, manchmal Probleme zu geben. Ohne spezielle Kennzeichnung von konventionell negativem Strom, fliesst der konventionelle Strom immer von Plus nach Minus. Wenn der Strom anstelle von I mit -I bezeichnet wird, dann ist eine gezeichnete Stromrichtung von Minus nach Plus legitim. Damit für den Einsteiger keine unnötige Verwirrung entsteht, gilt hier stets der Stromrichtungspfreil von Plus nach Minus.

Wie alle Elektronik-Minikurse legt auch dieser hier grossen Wert auf die praktische Umsetzung. Es wird ein Problem vorgestellt, das auftritt, wenn man mit so genannten Experimentier-Steckboards. Dazu gehört das Kapitel "UGBW: Experimentieren mit höheren Frequenzen - Probleme".

All diese Inhalte machen diesen Elektronik-Minikurs umfangreich. Dies ist unvermeidbar, weil diese Inhalte in der elektronischen Realität gemeinsam betrachtet werden müssen. All diese Eigenschaften beim Einsatz von Schaltungen mit Operationsverstärkern werden hier mit Bild und Wort vermittelt. Ich versuche den Inhalt lebendig zu gestalten und so wird die Elektronik erfahrbar, wenn der Azubi bereit ist, selbst mit dem Gelernten praktisch zu experimentieren. Simulieren mittels Software ersetzt das Experimentieren nicht! Trotzdem hat beides seine Daseinsberechtigung. Mehr zu diesem Thema liest man in Simulieren und Experimentieren, ein Vorwort von Jochen Zilg. Die Mathematik halte ich so knapp wie nötig. Dazu gibt es genügend Literatur die diesen und die weiteren Elektronik-Minikurse zum Thema Operationsverstärker ergänzen.

Ich möchte bei dieser Gelegenheit auf die folgenden Grundlagenkurse über Operationsverstärker von Patrick Schnabel (Inhaber des Elektronik-Kompendium) aufmerksam machen. Wenn man noch nichts oder nur sehr wenig über Operationsverstärker weiss, dann empfiehlt sich der Einstieg mit diesen Grundlagen. Sie vermitteln u.a. das Wissen wie man einfache invertierende und nichtinvertierende Verstärkerschaltungen berechnet. Die Inhalte sind anschaulich und praxisbezogen gestaltet. Man findet diese Seiten in:

Wichtiger Hinweis! Im Laufe der Jahre stellte ich fest, dass es immer wieder schwierig ist, die Eigenschaft der virtuellen Masse oder der virtuellen Spannung anschaulich mit Worten zu erklären. Es zeigte sich allerdings, dass es eine relativ einfache Sache ist, die verstanden werden muss. Danach ist für den Azubi, ob Lehrling oder Student, das Problem vom Tisch. Damit auch der Leser dieses Opamp-Minikurses das Hinunterfallen des Groschens erleben kann, bevor er hier weiterliest, bitte ich darum für kurze Zeit zum Kapitel "Wie kommt es zur virtuellen Masse (GND)?" umzuschalten in:

• Operationsverstärker III

Falls augenblicklich zum Studium nur wenig Zeit zur Verfügung steht, kann man sich das vertiefte Thema zur virtuellen Spannung in Operationsverstärker III auch später vornehmen, falls es auf Grund der persönlichen Vorbildung notwendig ist. Eine Entscheidung die man selber treffen muss.

  2.   Der virtuelle GND oder die virtuelle Spannung bei der invertierenden Verstärkung

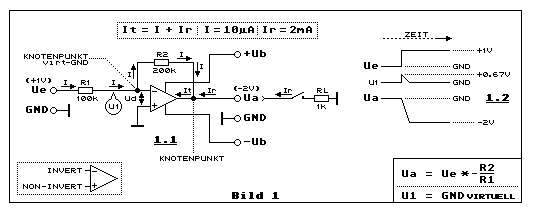
Da wir Bild 1 mit viel Text zwischen Kapitel 2.0 bis und mit 2.5 ständig benötigen, sollte man Bild 1 in einem seperaten Fenster darstellen oder vielleicht sogar ausdrucken, vor allem bei kleinen Monitoren um leichter zu lernen. Bild 1 jetzt anklicken!

Teilbild 1.1 illustriert den invertierenden Verstärker. Der nichtinvertierende Eingang des Opamp ist mit GND referenziert, wobei die Schaltung im Dual-Supply-Mode gespiesen wird mit +Ub, -Ub und GND. Wenn +Ub gleich gross ist wie -Ub, nennt man die Speisung auch symmetrisch. GND liegt dann in der Mitte zwischen +Ub und -Ub, was üblich ist. Der GND-Pegel ist hier die Arbeitsspannung, der Arbeitspunkt oder die Referenzspannung, wie man es auch immer zu nennen pflegt.

Nun wollen wir wissen, wie gross die Spannung U1 am invertierenden Eingang ist. U1 bezieht sich wie Ue und Ua ebenso auf GND. Wir wollen dabei gleich noch etwas wissen, nämlich ob U1 abhängig von der Eingangsspannung Ue ist. Da der nichtinvertierende Eingang mit GND verbunden ist, entspricht U1 ebenso dem GND-Pegel, weil die Differenzspannung Ud = 0 V ist, wenn Ue einen stationären Pegel hat oder Ue sich relativ zur Geschwindigkeit des Opamp nur langsam ändert. Anders formuliert: Die Signalfrequenz an Ue ist wesentlich niedriger als die Grenzfrequenz, gegeben durch die UGBW und Verstärkung, definiert durch R2/R1 und auch durch die Anstiegsgeschwindigkeit (Slewrate) der Opampschaltung. Die Slewrate bestimmt die Grenzfrequenz bei einer grossen Ausgangsspannung, während die UGBW bei einer niedrigen Ausgangsspannung begrenzt. Zunächst mit einfachen Worten auf den Punkt gebracht.

Die Angelegenheit der virtuellen Spannung und des virtuellen GND wird in Operationsverstärker III in Verbindung mit dem Einschwingvorgang vertieft thematisiert. Dort liest man auch wie es denn überhaupt zu einer solch kleinen Spannung Ud kommt, so dass man sie als 0 V unter den genannten Voraussetzungen bezeichnen kann.

Einschwingvorgang: In vielen Applikationen liest man von Einschwingvorgang und so auch in meinen Opamp-Minikursen. Dies erweckt leider eine etwas ungeeignete Vorstellung, weil bei einer reinen Verstärkerschaltung gar nichts einschwingt. Bei einer steilflankigen Änderung der Ausgangsspannung wirkt die interne hohe Verstärkung, die so genannte Leerlauf-Verstärkung (Open-Loop-Gain), verzögernd. Dadurch entsteht zunächst eine differenzielle Eingangsspannung U1, die dann anschliessend zurückgeht auf fast 0 V. Nur dann, wenn die Opampschaltung ein aktives Filter ist, mit einer gewissen Güte, bzw. geringe Dämpfung, gibt es einen echten Einschwingvorgang zwischen den beiden Opamp-Eingängen. Mehr zur Theorie des Einschwingvoganges liest man hier im Wiki unter Einschwingzeit.

Da die praktische Realisierung einer Verstärkerschaltung nie ideal ist, kann es, wenn auch kaum sichtbar auf dem Oszilloskopen, ein Einschwingvorgang geben, weil parasitäre Kapazitäten und ebenso Induktivitäten beim Vorgang "mitmischen". Um dies zu beobachten, muss man beim Versuch eine relativ hohe Impulsfrequenz an Ue einstellen, damit man an U1 den Einschwingvorgang beobachten kann. Das Fazit ist, dass der Begriff Einschwingvorgang gar nicht so falsch ist, wie manche denken, weil man es stets mit realen Verstärkerschaltungen mit Nebeneffekten zu tun hat. Wir kommen jetzt zu den Details...

2.1   Sprunghafte Änderung von Ue und die Folgen

Wir setzen den Fokus jetzt auch auf Teilbild 1.2. Ue liegt zunächst auf 0 VDC, also auf dem GND-Pegel. Nun schalten wir Ue sehr schnell auf +1 VDC. Da Ua im ersten Augenblick noch 0 V (GND-Pegel) hat, springt Ud bzw. U1 (weil nichtinv.Eingang = GND) kurzzeitig auf den Wert:

  U1 = Ud = Ue * (R2 / (R2 + R1))
  U1 = Ud = 1V * (200k / (200k + 100k)) = 0.67V

Warum sind es 0.67 V? Im ersten Augenblick nach dem Spannungssprung an Ue sieht es so aus, als ob der Opamp gar nicht existiert. Er hat mit seiner Arbeit noch gar nicht begonnen. R1 und R2 wirken noch als passive Spannungsteiler zwischen Ue und Ua (noch GND-Pegel), wie dies oben die Formel ausdrückt. Unmittelbar nach diesem Sprungereignis beginnt der Opamp mit seiner Arbeit und regelt Ua so, bis die Bedingung Ud = 0 V erfüllt ist.

Wegen der hohen Leerlaufverstärkung (Open-Loop-Gain), der starken Gegenkopplung mit R1 und R2 (niedrige Verstärkung, Closed-Loop-Gain) und der hohen Reaktionsgeschwindigkeit des Opamp sinkt die Ausgangsspannung Ua rasch ab auf negative Spannungswerte. Dadurch reduzieren sich Ud und U1 ebenso rasch. Ua ändert sich so lange, bis die Differenzspannung Ud praktisch 0 VDC erreicht hat. Dies ist dann der Fall, wenn sich im vorliegenden Beispiel Ua auf -2 VDC eingestellt hat.

Wieso sind es -2 VDC? Die virtuelle Spannung U1 liegt jetzt (fast) auf GND-Pegel, also 0 VDC. Die Spannung von Ue = +1 VDC liegt somit auch über R1. Der Strom von Ue über R1 und R2 in Richtung Ua bleibt gleich gross, weil der sehr geringe Biasstrom am invertierenden Eingang vernachlässigt werden kann. Da R2 doppelt so gross ist wie R1 und über R1 die Spannung von 1 VDC liegt, muss logischerweise über R2 eine Spannung von 2 VDC liegen. Da R2 links auf 0 VDC (virtueller GND, U1) liegt, muss Ua folgerichtig eine Spannung von -2 VDC haben. So einfach ist das. Wie man die Ausgangs- aus der Eingangsspannung berechnet, siehe Formel unten rechts in Bild 1.

Wichtig! Es muss einem nur klar werden, dass der gegengekoppelte Opamp immer zum Ziel hat, eine ihm aufgezwungene Differenzspannung Ud, so schnell er eben kann, fast vollständig zu beseitigen. Dies ist seine eigentliche regelungtechnische Aufgabe, die durch die sehr hohe (innere) Leerlaufverstärkung (Open-Loop-Gain) zustande kommt. Mehr dazu liest man in Operationsverstärker III im Kapitel "Wie kommt es zur virtuellen Masse (GND)?".

Die invertierende Verstärkerschaltung kann aber auch dämpfen, nämlich dann wenn R2 kleiner ist als R1. Eine solche aktive Dämpfung macht dann Sinn, wenn der Ausgangswiderstand von Ua besonders niederohmig sein soll. Wenn R1 und R2 gleich gross sind, invertiert die Schaltung in Bild 1 mit einer Verstärkung von -1. Die Verstärkung ist wegen der Spannungsinversion immer negativ.

Bei mittelschnellen Opamps liegt die Anstiegsgeschwindigkeit im 100ns- bis in den µs-Bereich innerhalb einer definierten Spannungsänderung. Der LF356 hat eine Anstiegsgeschwindigkeit von 12 V/µs. Das bedeutet, wenn am Eingang ein sehr schneller Spannungssprung erfolgt, ändert der LF356 seine Ausgangsspannung mit einer maximalen Geschwindigkeit von 12 V pro Mikrosekunde. Mann nennt diese Anstiegsgeschwindigkeit Slewrate. Im eingeschwungenen Zustand des Opamp hat Ud immer einen praktischen Wert von 0 V, und dies unabhängig von Ue. Praktisch bedeutet hier, dass Ud nicht exakt 0 V sein kann, weil die Leerlaufverstärkung des Opamp nicht unendlich hoch ist. Sie ist sogar stark frequenzabhängig, d.h. je grösser die Signalfrequenz am Eingang ist, um so niedriger ist Leerlaufverstärkung und damit das Verhältnis von ihr zur Verstärkung, die durch die R2/R1-Gegenkopplung definiert ist. Diese Verstärkung nennt man Closed-Loop-Gain. Ist dieses Verhältnis klein, misst man auch eine entsprechend grosse Differenzspannung Ud. Man studiere dies in einem Opamp-Datenblatt und man teste dies selbst an einem Experiment. Dies beeindruckt am meisten. Dieser dynamische Einschwingvorgang wird auch in Operationsverstärker III thematisiert.

Weil der nichtinvertierende Eingang beim Opamp mit GND verbunden und Ud = 0 V ist, liegt der invertierende Eingang (U1) ebenfalls auf GND-Potential. Da dieser U1-Spannungszustand jedoch durch den Regelvorgang der Gegenkopplung eines Verstärkers mit hoher Leerlaufverstärkung zustande kommt und U1 nicht wirklich mit GND identisch ist, nennt man diesen GND-Pegel am invertierenden Eingang, die virtuelle Masse oder den virtuellen GND. Um die Ausgangsspannung Ua zu berechnen, gilt folgende Knotentregel:

  (Ue / R1) + (Ua / R2) = 0

Daraus folgt das Ergebnis:

  Ua = Ue * -(R2 / R1)
  Ua = 1V * -(200k / 100k) = -2V

Theoretisch gilt die Knotenregel (der Knoten an dem gleich viel Strom zu- und abfliesst: invertierender Eingang) und die Berechnungsformel für die Verstärkung nur dann exakt, wenn die Leerlaufverstärkung des Opamp unendlich hoch wäre. Dies gibt es natürlich nicht, wie bereits weiter oben erklärt ist. Trotzdem ist für die meisten Anwendungen diese Formel genügend präzise, weil die Leerlaufverstärkung in der Regel um viele Grössenordnungen grösser ist als die gegengekoppelte Verstärkung, gegeben durch R2/R1. Es ist aber sehr wichtig, dass einem klar ist, dass die sehr hohe Leerlaufverstärkung von Opamps nur bei DC-Anwendungen und bei Anwendungen mit, relativ zur UGBW, niedrigen Frequenzen gilt. Man sollte dazu im Datenblatt eines Opamp das Diagramm Open-Loop-Frequency-Response studieren! Da wir es hier u.a. mit dem LF356 zu tun haben, gleich das zugehörige Diagramm. Man erkennt, wie die Linie zum LF156 (LF356) die 0dB-Linie (Verstärkung=1) bei 5 MHz kreuzt. Das ist UGBW-Frequenz. Die sehr hohe Leerlaufverstärkung gilt nur gerade zwischen DC und deutlich weniger als 100 Hz. Dies ist die Folge der (inneren) Frequenzgangkompensation, die garantiert, dass der Opamp bis hinunter auf Verstärkung=1 stabil arbeitet. Mehr dazu im nächsten Kapitel.

Knotenregel nochmals: Dazu nochmals Bild 1. Es geht dabei um die Ströme I, Ir und It. Dazu gehören die Spannungsangaben in Klammern. Wenn Ue = +1 V, dann fliesst über R1 zum invertierenden Eingang (Knoten, virtueller GND) ein Strom I von 10 µA, gegeben durch die Spannung von 1 V über R1 = 100 k-Ohm. Dieser Strom I von 10 µA fliesst weiter durch R2 = 200 k-Ohm zum Ausgang des Opamp. Über R2 liegt eine Spannung von 2 V. Weil der invertierende Eingang (Knoten) virtuell GND-Potenzial hat, liegt an Ua folgerichtig die negative Spannung von -2 V. Der Opamp-Biasstrom ist auch in der hier angewandten Praxis und nicht nur in der vereinfachten Theorie vernachlässigbar klein. Deshalb gilt an dieser Stelle die einfache Knotenregel, betreffs identischem Ein- und einen Ausgangstrom I beim invertierenden Eingang des Opamp. Siehe I-Pfeile in Bild 1.

Bisher gibt es an Ua noch keine Last. It in Richtung Opamp-Ausgang, ist also nur I, gegeben durch die Knotenregel. Wir schalten jetzt den Lastwiderstand RL = 1 k-Ohm zwischen Ua und GND mit einem Strom Ir = 2 mA. Weil GND positiver ist als -2 V, fliesst Ir vom GND via RL zum Ausgang des Opamp. Dabei addiert sich Ir (r von RL) mit I zu It (t = total) mit 2.01 mA. Dabei ergibt sich ein weiterer Knoten. Nämlich an der Stelle wo Ir und I (zufliessend) sich zu It (wegfliessend) in Richtung Opamp-Ausgang addieren.

Etwas verwirrend ist die Formulierung, dass ein Strom in einen Ausgang fliesst. Das ist jedoch nur so lange der Fall, als man sich nicht vorstellt, dass der Ausgang eines Opamps eine Gegentaktendstufe (Bild: Wiki) besitzt, die sowohl als Stromquelle (NPN-Stufe) und als Stromsenke (PNP-Stufe) arbeitet.

Wenn Ue an Stelle einer positiven eine negative Spannung aufweist, resultiert an Ua eine positive Spannung. An der Knotenpunkt-Tatsache beim invertierenden Eingang ändert sich nichts, ausser dass alle Strompfeile I,Ir und It um 180 Grad gedreht sind.

2.2   Leerlaufverstärkung, Differenzspannung und Frequenz

Bei dem bereits etwas betagten Opamp LF356, der aber für sehr viele Anwendungen auch noch heute aktuell ist, beträgt die Leerlaufverstärkung zwischen DC und etwa 50 Hz 105 dB (~180'000). Selbst dann, wenn man eine gegengekoppelte Verstärkung von 40 dB (100) oder auch mehr hat, ist das Verhältnis zur Leerlaufverstärkung bei dieser niedrigen Frequenz so gross, dass die differenzielle Eingangsspannung Ud praktisch 0 V ist. Bei einer Frequenz von 1 kHz beträgt die Leerlaufverstärkung allerdings nur noch 70 dB (~3200). Auch das ist noch viel für eine gegengekoppelte Verstärkung von 40 dB (100) und Ud bleibt noch immer vernachlässigbar niedrig. Bei 20 kHz - diese Bandbreite empfiehlt sich für HIFI-Audioverstärker - beträgt die Leerlaufverstärkung gerade noch 48 dB (250). Hier wäre die einfache Berechnungsformel (Bild 1) für die gegengekoppelte Verstärkung von 40 dB (100) doch etwas ungenau. Realisiert man jedoch einen Audioverstärker mit einer Bandbreite von eben diesen 20 kHz, d.h. eine Amplitudendämpfung von 3 dB bei dieser Grenzfrequenz, so darf man getrost eine gegengekoppelte Verstärkung von 40 bis 46 dB mit diesem LF356 mit der einfachen Formel (Bild 1) dimensionieren. Es spielt für eine Audioanwendung überhaupt keine Rolle, dass bei der Grenzfrequenz Ud nicht mehr bis auf fast 0 V hinunter geht. Diese Abweichung verursacht übrigens die Dämpfung von 3 dB bei der Grenzfrequenz.

Nochmals zum Audioverstärker. Wir wählen eine Verstärkung von 200 (46 dB). Multipliziert man diese gegengekoppelte Verstärkung von 200 mit der wirksamen Frequenzbandbreite von 25 kHz, kommt man auf den Wert der UGBW von 5 MHz. Damit wissen wir auch, wie die nutzbare Frequenzbandbreite (Grenzfrequenz fg, fc [c = cuttoff] und oft auch als GBW bezeichnet) aus der Unity-Gain-Bandbreite (UGBW) und der gegengekoppelten Verstärkung berechnet wird:

  fg = fUGBW / GainClosed-Loop
      Beispiel für den LF356:   25kHz = 5000kHz / 200
      Beispiel für den TL071:   15kHz = 3000kHz / 200

Wir wissen nun, dass bei höheren Frequenzen Ud nicht mehr Null sein kann. Es stellt sich die Frage, ob dann die Bezeichnung virtueller GND noch angebracht ist. Die typische Radio-Eriwan-Antwort: Im Prinzip ja, weil es kommt auf die Anwendung an. Der Spannungsmittelwert der relativ hochfrequenten AC-Spannung Ud beträgt 0 V. Ist die Nutzfrequenz nicht allzu nahe bei der Grenzfrequenz, verhält sich der Regelkreis, der diese Closed-Loop-Verstärkung bedingt, so, dass man praxisbezogen noch von virtuellem GND reden kann. Die Angelegenheit mit dem virtuellen GND ist etwas relativ...

2.3   Grenzfrequenz, Slewrate und Leistungsverbrauch

Wir haben zwei Arten der Geschwindigkeitsgrenzen des Opamp kennen gelernt. Die eine ist die Slewrate, die maximale Anstiegsgeschwindigkeit, mit der die Ausgangsspannung einer sprunghaften Änderung der Eingangsspannung folgen kann. Die andere Art ist die Grenzfrequenz, welche durch die UGBW und durch die gegengekoppelte Verstärkung (Closed-Loop-Gain) bedingt ist.

Da stellt sich die Frage, bei welchen Kriterien gilt die Slewrate und bei welchen die Unity-Gain-Bandbreite (UGBW) mit der Verstärkung als Limit. Das ist gar nicht so einfach. Es kommt ganz darauf an, wie die Slewrate und die Unity-Gain-Bandbreite zusammenpassen. Es gibt z.B. Opamps mit besonders niedrigem Leistungsverbrauch und recht hoher Unity-Gain-Bandbreite. Dies äussert sich dann darin, dass selbst bei relativ hoher gegengekoppelter Verstärkung, die Frequenzbandbreite trotzdem relativ hoch ist. Allerdings nur dann, wenn die Amplitude am Ausgang klein bleibt. Bei relativ grosser Amplitude, würde man u.U. ein stark verzerrtes Sinussignal auf dem Bildschirm des Oszilloskopen beobachten. Diese Verzerrung wird dann durch die zu niedrige Slewrate verursacht und diese Slewrate kann einfach wegen dem zu geringen Leistungsverbrauch der Betriebsspannung nicht grösser sein. Legt man Wert darauf, dass bei relativ hoher Grenzfrequenz der Opamp auch bis fast zur Betriebsspannung unverzerrt ausgesteuert werden kann, muss man auf leistungsarme Opamps verzichten. Für den niederfrequenten Bereich (z.B. Audio) haben sich die tradionsreichen JFET-Opamp LF356 (single), TL071 (single), TL072 (dual) und TL074 (quad) sehr gut bewährt. Diese TL07x-Familie ist von Texas-Instruments (TI) und ebenso die Excalibur-Familie TLE2021 (single), TLE2022 (dual) und TLE2024 (quad). Seit National-Semiconductor-Corporation (NSC) die Halbleiterproduktion eingestellt hat, wird der LF356 ebenfalls von TI produziert. Es gibt längst modernere Opamps, welche bei geringerem Leistungsverbrauch höhere Slewrates und UGBW haben im Vergleich zu diesen hier. Dies muss man selbst evaluieren (Aussage: 2017).

Wir wissen bereits wie man die Grenzfrequenz aus der UGBW, aber noch nicht wie man die Slewrate aus der Frequenzbandbreite und der Amplitude berechnet. Es setzt voraus, dass man weiss wie hoch die maximale Frequenz und die maximale Amplitude am Ausgang eines Opamp sein soll. Dann berechnet man die Slewrate mit der folgenden Formel:

   SR = 2 * PI * fg * Up

SR ist die Slewrate in V/µs, fg ist die Grenzfrequenz in MHz und Up (p = peak) ist die Sinus-Scheitelwertspannung.

Berechnungsbeispiel: Man benötigt einen Opamp für eine maximale Ausgangsspannung von Up = 10 Vp und eine maximale Frequenz von 20 kHz. Dies ergibt eine Slewrate von 1.26 V/µs. Warum gerade 10 Vp? Einfacher Grund, es gibt A/D-Wandler mit maximalen Eingangsspannungen von ± 10 V und die Digitalisierung von analogen Signalen ist ja nicht gerade eine seltene Anwendung.

Wir gehen noch ein Schritt weiter und verlangen von diesem Opamp eine Verstärkung von 100 (40 dB). Bei einer Frequenz-Bandbreite von 20 kHz muss der gesuchte Opamp eine UGBW von mindestens 2 MHz aufweisen. Wir entscheiden uns für den altbekannten und preiswerten LF356 und bemerken, dass er sich mit einer Slewrate von 12 V/µs und einer Unity-Gain-Bandbreite von 5 MHz hervorragend eignet, weil er liefert eine nutzbare Bandbreite von 50 kHz (Gain = 100) und erlaubt bei einer maximalen Sinus-Scheitelwertspannung von 10 Vp eine maximale Frequenz von 190 kHz. Wozu diese hohe Slewrate gut sein soll, kann man sich fragen. Einfache Antwort: Diese Slewrate erzeugt bei einer maximalen Audio-Frequenz von 20 kHz, aber auch bei 50 kHz, noch kein nennenswerter Klirrfaktor.

Wenn die Verstärkerschaltung mit einer Batterie gespiesen wird und ein Opamp in Frage kommen muss, der weniger Leistung verbraucht, muss man sich nach einem Lowpower-Opamp mit einer niederigeren Slewrate umsehen, die aber venünftigerweise noch immer etwa doppelt so hoch ein sollte, wie man errechnet hat, also etwa 3 bis 3.5 V/µs. Da kämen z.B. TL061 (single), TL062 (dual) oder TL064 (quad) in Frage. Allerdings rauscht diese Opamp-Familie wesentlich mehr als die TL07x-Familie. Das Rauschen ist Thema des Elektronik-Minikurses Rauschdämpfung mit Tiefpassfilter. Es gibt modernere Opamps bei denen die widersprechenden (antagonistischen) Qualitätsmerkmalen von Leistungsverbrauch, Rauschen, Slewrate und UGBW weniger drastisch sind, wie z.B. bei der weiter oben genannten Excalibur-Familie. Es empfiehlt stets auch immer ein Blick über den Gartenzaun, zu andern Opamp-Hersteller, wie z.B. Linear-Technnology. Dazu gleich ein Datenblatt zur TLE-Excalibur-Familie.

2.4   Eine kleine Software-Unterstützung für die Berechnung der Slewrate

• What's All This Slewrate Stuff, Anyhow?
  Eingabe: Frequenz-Bandbreite, Amplitude
  Resultat: Slewrate

2.5   Anstelle GND eine variable Referenzspannung

Bild 2 zeigt uns, worin sich diese Schaltung von der in Bild 1 unterscheidet:

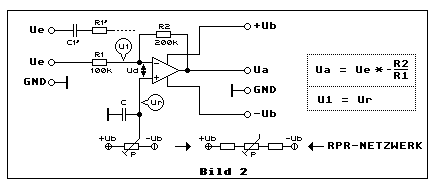
Der nichtinvertierende Eingang des Opamp ist nicht wie in Bild 1 mit GND verbunden. Hier kann man die Referenzspannung Ur mit dem Trimmpotmeter P zwischen +Ub und -Ub einstellen. Man kann Ur so einstellen, dass Ua exakt auf den GND-Pegel abgeglichen ist oder man stellt an Ua ganz bewusst einen andern Spannungswert ein. Wozu soll das denn gut sein?

Wenn eine AC-Spannung am Eingang Ue mit einer DC-Spannung (DC-Offsetspannung) überlagert ist, kann man mit P diese DC-Offsetspannung kompensieren, damit die AC-Spannung Ua sich auf GND bezieht. Der Opamp arbeitet hier bei als invertierender Verstärker und als Subtrahierer. Diese Methode ist vor allem dann die richtige Lösung, wenn sehr niederfrequente Eingangsspannungen (quasi-stationäre Spannungen) mit möglichst konstanter Amplitude oder sogar DC-Spannungen verstärkt werden müssen. Für reine AC-Anwendungen gibt es die alternative Möglichkeit den DC-Anteil mittels eines in Serie zu R1 geschalteten Kondensators zu entkoppeln. Dieses R1'*C1'-Glied wirkt dann als passives Hochpassfilter mit einer typisch unteren Grenzfrequenz. Ein Beispiel dazu, siehe kurz Teilbild 8.1 mit R1 und C1.

Das RPR-Netzwerk: Rechts von P ist P gleich noch einmal, jedoch mit je einem Seriewiderstand in Richtung +Ub und -Ub erweitert. Wenn man diese Schaltung benutzt, verkleinert man den Einstellungsbereich von P. Dies erleichtert den präzisen Abgleich enorm, wenn es kleine DC-Offsetspannungen sind, die möglichst genau auf Null kompensiert sein müssen. Wenn die DC-Offsetspannung nur eine bestimmte Polarität haben kann, darf man das eine Ende des Potmeter (oder der eine Widerstand) mit GND verbinden. Ist nur eine positive DC-Offsetspannung an Ue möglich, liegt das Potmeter (mit den Widerständen) zwischen +Ub und GND, ist sie nur negativ möglich, dann zwischen -Ub und GND.

Kondensator C unterdrückt eine allfällige mittel- bis hochfrequente störende Spannungseinkopplung in die Verstärkerschaltung über den nichtinvertierenden Eingang. Dies ist besonders dann empfehlenswert, wenn es in der Nähe AC-Spannungen hat, welche parasitär kapazitiv einkoppeln können, z.B. wegen parallel liegenden Leiterbahnen. Beim Printdesign muss man hierbei sehr aufpassen, ob man gewisse Leitungen parallel verlegen darf oder nicht. Parallele Leitungen erzeugen höhere parasitäre Kapazitäten. Im Falle von hochfrequenten Störspannungen oder auch niederfrequente Störspannungen mit steilen Flanken, empfiehlt sich für C ein Keramik-Multilayer-Kondensator (abk.: KERKO). Siehe auch weiter unten Kapitel 6.1 "Wenn Opamps andere Opamps stören" mit Bild 13 und Kapitel 8 "UGBW: Experimentieren mit höheren Frequenzen - Probleme" mit den Bilder 15 und 16. Ebenso empfehlenswert Operationsverstärker IV: Störprobleme.

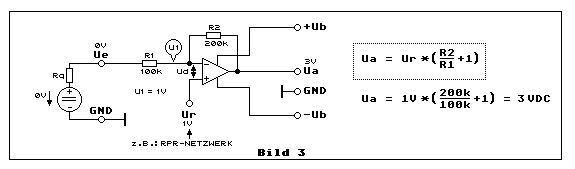
Grundsätzlich ist dies die selbe Schaltung wie die in Bild 2. Wir wollen uns hier damit beschäftigen, wie sich die Referenzspannung Ur auf die Ausgangsspannung Ua auswirkt. Das ist ganz einfach, wenn man erkennt, dass man es von der Seite des nichtinvertierenden Eingangs (Ur) mit der Berechnungsformel für nichtinvertierende Verstärkung zu tun hat. Man muss sich zunächst bloss vorstellen, dass Ue GND-Potential hat. Die extern angeschlossene Spannungsquelle hat 0 VDC und der Innenwiderstand Rq ist im Verhältnis zu R1 sehr niederohmig. Wenn Ur z.B. einen Wert von 1 VDC hat, hat Ua, gemäss vorliegender Dimensionierung mit R1 und R2, einen Wert von 3 VDC. Siehe kleingeschriebene Zahlen. Es gilt dazu die Formel im punktierten Rahmen, wobei Ue = 0 VDC ist.

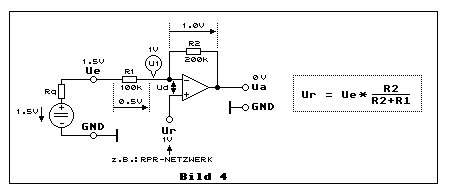
Bild 4 unterscheidet sich von Bild 3 darin, dass an Ue eine DC-Spannung liegt. Wir überlegen uns jetzt, wie gross muss diese DC-Spannung sein, damit die DC-Spannung an Ua von 3 VDC (Bild 3) auf den GND-Pegel von 0 VDC kompensiert wird. Von der Ue-Seite haben wir es mit der invertierenden Verstärkung zu tun. Bei vorliegender Dimensionierung von R1 und R2 ergibt sich eine Eingangsspannung von Ue = 1.5 VDC. Fassen wir also zusammen: Wenn Ue = 1.5 VDC und Ur = 1 VDC ergibt sich Ua = 0 VDC.

Betrachten wir dies jetzt unter dem Aspekt der virtuellen DC-Spannung von U1. Weil Ud = 0 VDC, ist U1 = Ur und Ur hat im vorliegenden Beispiel eine Spannung von 1 VDC. Weil Ue = 1.5 VDC und U1 = 1 VDC, entsteht über R1 eine Spannung von 0.5 VDC. Dieser Spannungsabfall über R1 erzeugt einen Strom. Dieser Strom fliesst aber ebenso durch R2 - der im vorliegenden Beispiel den doppelten Wert von R1 hat - zum Ausgang Ua des Opamp. Also entsteht an R2 ein Spannungsabfall von 1 VDC. Diese Spannung subtrahiert sich von der virtuellen Spannung U1 = 1VDC und so entsteht am Ausgang des Opamp Ua = 0 VDC, oder eben GND-Potential.

Wir haben in diesem Gedankenexperiment den umgekehrten Vorgang durchgespielt. Es begann damit, sich zu fragen, wie sich Ur auf Ua auswirkt. Praktikabler ist es allerdings zu wissen, wie gross Ur sein muss, um eine DC-Offsetspannung an Ue zu kompensieren. Dem Leser sei empfohlen andere Werte für Ue einzusetzen und zu berechnen wie gross Ur sein muss um Ua auf 0 VDC zu kompensieren. Man kann dabei auch andere Werte für R1 und R2 wählen. Besonders empfehlenswert ist es solches an einer echten Testschaltung zu erproben und erfahren! Die Berechnungsformel steht im punktierten Kasten in Bild 4.

Was bedeutet DC-Offsetspannung: Betreffs der DC-Spannung an Ue liest man hier oft DC-Offsetspannung. Das kommt daher, dass es diese DC-Spannung geben kann, wenn eine AC-Spannung übertragen und verstärkt wird, jedoch mit einer DC-Spannung überlagert ist. Dies ist die typische Situation einer DC-Offsetspannung.

2.6   Extra-Link zum Thema virtuelle Spannung

Dieser Elektronik-Minikurs zeigt wo es beim Opamp zur so genannten virtuellen Spannung oder virtuellem GND kommt, nämlich stets beim invertierenden Eingang des gegengekoppelten Opamp. Es wird aber bloss angedeutet wie es zu diesem Effekt kommt. Vertieft wird dies in Operationsverstärker III.

2.7   Der Eingangswiderstand bei der invertierenden Verstärkung

Wir haben es bis hier mit der invertierenden Verstärkerschaltung zu tun. Nun wollen wir uns überlegen, wie gross der Eingangswiderstand an Ue ist. Wir können dazu irgend eine Schaltung von Bild 1 bis Bild 4 betrachten. Wir wissen nun, dass U1 der virtuelle GND oder die virtuelle Referenzspannung von Ur ist und dass sich U1 nicht ändert, wenn sich Ue ändert, ausser Ue ändert sich schneller als der Opamp reagieren kann. Diesen allerdings sehr kurzen Zeitabschnitt interessiert uns hier nicht.

Wenn U1 der virtuellen Spannung von GND entspricht, können wir uns ebenso vorstellen, dass R1 zwischen dem Ue-Anschluss und dem richtigen GND verbunden ist und es leuchtet sogleich ein, dass der Eingangswiderstand an Ue dem Wert von R1 entspricht. Dies ist so, weil der GND-Pegel vom Strom oder von einer Stromänderung via R1 nicht beeinflusst wird. Warum der virtuelle GND am nichtinvertierenden Eingang die selbe Eigenschaft wie der richtige GND hat, kommt vom Ausgang des Opamps. Dieser stellt seine Ausgangsspannung durch den Regelvorgang so ein, dass der Strom von Ue über R1 und R2 nach Ua genau so gross ist, dass der virtuelle GND (die virtuelle Spannung) am nichtinvertierenden Eingang konstant bleibt. Dies funktioniert natürlich nur so gut, wie der Opamp im linearen Bereich arbeitet, also seine Ausgangsspannung Ua im positiven und negativen Spannungsbereich nicht zu hoch wird. Diese Grenzen entnimmt man dem Opamp-Datenblatt. Dazu kommt, dass der Strom von der Endstufe des Opamp verarbeitet werden muss. Auch diese Grenze liest man im Opamp-Datenblatt.

Wenn Ur, und damit U1, einen andern Spannungswert als den GND-Pegel hat, gilt die selbe Betrachtung. Man stelle sich dann eben vor, dass R1 zwischen Ue und Ur liegt, wobei die Spannungsquelle an Ur im Verhältnis zu R1 dann allerdings sehr niederohmig sein muss. Auch hier gilt, dass der Eingangswiderstand an Ue dem Wert von R1 entspricht. Wir können damit zusammenfassen: Bei einer invertierenden Verstärkerschaltung entspricht der Eingangswiderstand immer dem Widerstand zwischen dem Signal-Eingang (Ue) und dem invertierenden Eingang der Verstärkerschaltung.

3.   Die virtuelle Eingangsspannung bei der nichtinvertierenden Verstärkung

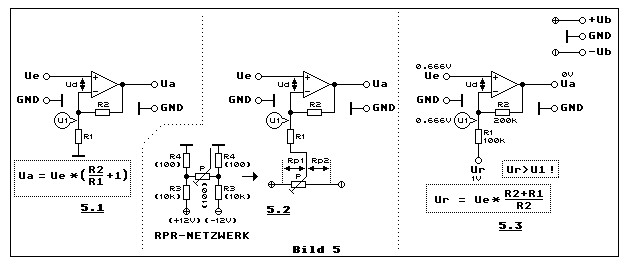
Teilbild 5.1 zeigt uns die einfache nichtinvertierende Verstärkerschaltung. Es gilt selbstverständlich auch hier, dass Ud im eingeschwungenen Zustand O V beträgt. U1 entspricht also Ue. U1 ist die virtuelle Eingangsspannung von Ue. Wenn Ue sich ändert passt U1 sich Ue an, allerdings auch hier nur mit der maximal möglichen Geschwindigkeit des Opamp.

Teilbild 5.2 unterscheidet sich von Teilbild 5.1 nur darin, dass die Schaltung durch die Einstellbarkeit der DC-Offsetspannung mit Trimmpotmeter P erweitert ist. Auch hier kann man, zwecks besserer Feineinstellung, P mit Seriewiderständen erweitern, wie dies weiter oben zu Bild 2 beschrieben ist. Bei dieser nichtinvertierenden Verstärkerschaltung hat diese Art der DC-Offsetspannungseinstellung gegenüber Bild 2 allerdings einen gravierenden Nachteil: Die Parallelsumme der beiden Teilwiderstände Rp1 und Rp2 addieren sich zu R1. Dies hat zur Folge, dass P an der Verstärkung Ua/Ue beteiligt ist. Verändert man P zwecks Einstellung der DC-Offsetspannung, verändert dies auch die Verstärkung. Soll der Einfluss von P auf die Verstärkung gering sein, muss der Widerstand von P signifikant niedriger sein als der Eingangswiderstand in Richtung invertierenden Eingang, und dies entspricht, wie wir jetzt wissen, dem Wert von R1. Um es noch einmal ganz klar werden zu lassen: Aus der Sicht von Ue (nichtinvertierend) ist der Eingangswiderstand praktisch unendlich hoch und aus der Sicht von Ur (invertierend) entspricht der Eingangswiderstand dem Wert von R1.

Es gibt einen einfachen und eleganten Trick, wenn nur niedrige DC-Offsetspannungen, z.B. im 1mV- bis 100mV-Bereich, kompensiert werden müssen. Hier bietet sich das Kompensationsnetzwerk aus R3, R4 und P an. Auch hier liegt, wie in Bild 2, das Trimmpot P in der Mitte eines Widerstandsnetzwerkes. Deshalb auch hier die Bezeichnung RPR-Netzwerk. Wenn R4 wesentlich niederohmiger als R3 ist und P etwa R4 entspricht, erreicht man einen sehr niederohmigen Quellwiderstand dieses RPR-Netzwerkes, ohne dass unnötig viel Strom durch P fliessen muss. Genau dies ist dann der Fall, wenn über R4 nur eine kleine Teilspannung der Betriebsspannung benötigt wird. Angenommen die Betriebsspannung beträgt ± 12VDC und über den beiden R4-Widerständen liegt für den DC-Offsetabgleich eine Spannung von bloss ±50 mVDC, dann haben die beiden R4-Widerstände je einen Wert von 100 Ohm, wenn die beiden R3-Widerstände Werte von 10-k-Ohm haben. Für P eignet sich ebenfalls ein Wert 100 Ohm. Man beachte die Widerstandswerte in Klammern.

BTW: Es versteht sich von selbst, dass für diesen Kompensationszweck +Ub und -Ub gut stabilisierte Spannungen sein müssen. Die üblichen Fixspannungsregler, z.B. 7812 und 7912 für ±12 VDC, reichen dafür jedoch meist aus. Diese Spannungsregler dienen gleichzeitig auch der Speisung der gesamten analogen Schaltung. Wenn diese Präzision nicht genügt, ist der Einsatz von hochstabilen Bandgap-Spannungsreferenzen angezeigt.

Man kann den Einfluss von P auf die Verstärkung noch unwirksamer machen, in dem man zwischen dem Ausgang von P (Schleifer) und dem Eingang zum R1 einen Impedanzwandler, also eine Opampverstärkerstufe mit Verstärkung +1, schaltet. Der Ausgangswiderstand des Impedanzwandlers ist extrem niederohmig. Aber auch diese Methode hat nicht nur Vorteile: Der zusätzliche Impedanzwandler ist eine zusätzliche Rauschspannungsquelle, und diese Rauschspannung wird mit R2/R1 mitverstärkt. Wenn man diese Methode einsetzt, muss man mittels zusätzlichen Kondensatoren am Ausgang des Impedanzwandlers dafür sorgen, dass die Rauschsspannung gut bedämpft wird. Mehr dazu liest man im Kapitel Die Ub/2-Referenz und der synthetische GND.

Teilbild 5.3 entspricht Teilbild 5.2 mit dem einzigen Unterschied, das Ur frei ist für eine externe Spannungsquelle, die ebenfalls unbedingt niederohmig sein muss, soll die Verstärkung, gegeben durch R2/R1, nicht verfälscht werden. Ähnlich zu Bild 4 befassen wir uns hier damit, wie gross Ur sein muss um eine DC-Offsetspannung an Ue zu kompensieren. Wir nehmen auch hier an Ur = 1 VDC, dann beträgt bei Ue = 0 VDC die Ausgangsspannung Ua = -2 VDC. Die positive Spannung an Ue muss einen Wert von 0.666 VDC haben, um an Ua eine positive Gegenspannung von +2 VDC zu erzeugen. Diese +2 VDC kompensiert die -2 VDC zu 0 VDC.

Die Berechnungsformel von Teilbild 5.3 ist mehr praxisorientiert als die von Teilbild 5.1, weil man hat in der Regel an Ue eine unerwünschte DC-Offsetspannung, z.B. überlagert auf einer AC-Spannung, die man kompensieren muss. Also stellt sich die Frage nach der Grösse von Ur und nicht von Ue, die gegeben ist.

3.1   Der Eingangswiderstand bei der nichtinvertierenden Verstärkung

Bild 5 zeigt uns drei nichtinvertierende Verstärkerschaltungen. Wir wollen uns überlegen, wie gross der Eingangswiderstand an Ue jeweils ist. Wir bemerken, dass der nichtinvertierende Eingang unbeschaltet ist. Beim idealen Opamp bedeutet dies, dass der Eingangswiderstand unendlich hoch ist. Die Realität zeigt ein etwas anderes Bild. Opamps mit bipolaren Transistoren nach den Eingängen können recht niederohmige Eingangswiderstandswerte haben. Beim NE5534, übrigens hervorragend geeignet für Audio-Vorverstärker mit niedriger Rauschspannung, wird der Eingangswiderstand mit bloss 50 bis 100 k-Ohm angegeben. Wobei dieser Wert stets ohne Gegenkopplung gilt. Bewirkt die Gegenkopplung eine niedrige Verstärkung relativ zur wesentlich höheren Leerlaufverstärkung, multipliziert sich dieser Eingangswiderstand in etwa mit dem Verhältnis der Leerlaufverstärkung zur gegengekoppelten Verstärkung. Daraus resultiert der effektive Eingangswiderstand. Wir wissen jetzt aber auch, dass die Leerlaufverstärkung frequenzabhängig ist, also gilt dies auch für den Eingangswiderstand: Je höher die Frequenz am Eingang Ue, um so niedriger der Eingangswiderstand. Dieser Effekt steht auch ganz klar in Zusammenhang mit Ud, dessen Wert im Idealfall Null, jedoch real frequenzabhängig ist.

Sind jedoch Darlingtonstufen, wie z.B. beim LM324 oder LM358 mit PNP-Transistoren, im Einsatz, kann der Eingangswiderstand weit im M-Ohm-Bereich liegen, ohne dass dabei Leerlaufverstärkung und die Verstärkung durch die Gegenkopplung berücksichtigt sind. Aber auch dies reisst noch niemanden vom Stuhl, wenn man die Eingangswiderstandswerte von JFET-Opamps, wie z.B. beim LF356, betrachtet. Hier liegt der Eingangswiderstand bei etwa 1 T-Ohm. (Es sei an dieser Stelle kurz angedeutet, dass es betreffs Opampeingänge noch andere wichtige Parameter gibt, wie DC-Offset- und DC-Bias-Strom.)

Diese nichtinvertierenden Eingänge von JFET- und MOSFET-Opamps eignen sich für den Anschluss hochohmiger Spannungsquellen, wie z.B. biomedizinische Signale (EMG, EEG, EKG). Auch intramuskuläre EMG-Spannungsquellen, welche Quellimpedanzen von vielen 100 k-Ohm bis in den unteren M-Ohm-Bereich haben können, eignen sich sehr gut. Dass hier nur JFET- oder MOSFET-Opamps in Frage kommen, hat noch den Grund, dass die Eingangsrauschströme um viele Grössenordnungen niedriger sind als bei Opamps mit bipolaren Eingängen. Diese Rauschströme multiplizieren sich an den Quellwiderständen zu Rauschspannungen. Allerdings muss man diese hochohmigen biomedizinischen Signale differenziell mit so genannten Instrumentations-Verstärkern messen. Wie und warum man dies macht, zeigen diese Elektronik-Minikurse Echter Differenzverstärker I, Echter Differenzverstärker II, Echter Differenzverstärker III und Echter Differenzverstärker IV ausführlich.

Es gibt neben den Bezeichnungen JFET- und MOSFET-Opamp auch noch die Bezeichnung BiFET-Opamp. Ein BiFET-Opamp hat am Eingang stets JFETs oder MOSFETs. Der ganze Rest kann aus bipolaren Transistoren (BJTs) bestehen. So z.B. der hier erwähnte LF356. Eingangsseitig JFETs und der Rest, ausser noch ein JFET, nur noch BJTs. Es gibt auch BiFET-Opamps, die ein- und ausgangsseitig MOSFETs, jedoch in der Schaltung dazwischen BJTs haben. Der Sinn war früher, weil man mit BJTs höhere Verstärkungsfaktoren erzielte. So z.B. beim CA3130.

4.   GND oder Referenzspannung, ja nach Art der Schaltung

Eine Verstärkerschaltung kann immer nur eine Ausgangsspannung liefern, welche maximal den Wert der Betriebsspannung hat. In der Praxis ist dies aber meist weniger. Hat eine Verstärkerschaltung bipolare Transistoren am Ausgang, reduzieren die einfachen oder mehrfachen Basis-Emitter-Übergänge der Transistoren die Amplitude am Ausgang. Besser eignen sich betreffs maximaler Aussteuerung Opamps mit MOSFET-Ausgangsstufen. Unbelastet oder nur sehr wenig belastet, erreichen die Ausgangsamplituden Werte der Betriebsspannung. Man nennt einen solchen Opamp-Ausgang einen Rail-to-Rail-Output. Eine kurze Erklärung dazu findet man in 555-CMOS: 50%-Duty-Cycle-Generator im Kapitel "Bipolare 555-Endstufe versus CMOS-555-Endstufe" illustriert mit Bild 1 am Beispiel einer bipolaren und CMOS-Ausgangsstufe eines NE555-, bzw. LMC555-Timer-IC.

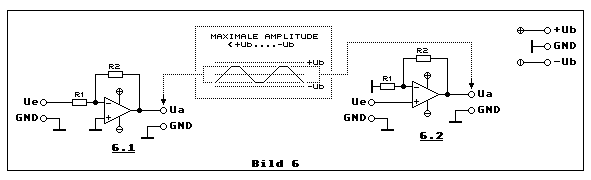
Auch der Eingangsspannung Ue sind durch die Betriebsspannung ±Ub Grenzen gesetzt. Dies muss man vor allem dann wissen, wenn die Schaltung bloss eine Verstärkung von 1 hat. In diesem Fall entspricht die Eingangsspannung der Ausgangsspannung, Ue = Ua. Diese Betrachtung betreffs Ue gilt aber nur bei der nichtinvertierenden Verstärkerschaltung Teilbild 6.2, bei der der Eingang des Opamps mit der Eingangsspannung Ue identisch ist (R1 entfernt). Dieses Problem mit dem Eingang besteht bereits bei niedriger Verstärkung von etwas mehr als 1 nicht, weil dann Ua vor Ue begrenzt, wenn Ue ansteigt.

Bei der invertierenden Verstärkerschaltung (Teilbild 6.1) erreicht der invertierende Eingang im schlimmsten Fall die Spannung von Ue nur sehr kurz, nämlich zu Beginn des Einschwingvorganges, falls sich die Eingangsspannung schneller ändert als der Opamp reagieren kann. Diese Angelegenheit ist weiter oben bereits beschrieben. Es ist sogar möglich, dass man mit einer invertierenden Verstärkerschaltung eine aktive Abschwächung realisieren kann. Wenn R1 z.B. 1000 mal grösser ist als R2, kann man aus einer Spannung Ue von z.B. 3300 VDC eine Spannung Ua von -3.3 VDC erzeugen. Auf diese Weise kann man sehr hohe Spannungen messen und weiterverarbeiten. Man muss dann allerdings einige Sicherheitsvorkehrungen treffen, auf die ich hier nicht weiter eingehe. Für Anfänger und Unerfahrene in der Anwendung von Hochspannung sollte dies sowieso kein (Bastel-)Thema sein!!!

GND und Arbeitspunkt: Es geht dabei um den Unterschied zwischen der Speisung mit nur einer Betriebsspannung +Ub (Single-Supply) oder mit zwei Betriebsspannungen ±Ub (Dual-Supply). Damit befassen wir uns in Bild 6, das in Teilbild 6.1 eine invertierende und in Teilbild 6.2 eine nichtinvertierende Verstärkerschaltung enthält. Beide werden mit Dual-Supply (±Ub) gespiesen. Dies bedeutet, dass die Ausgangsspannungen theoretisch maximal die positive und negative Betriebsspannung erreichen können. Jede Verstärkerschaltung muss aber auch referenziert sein. Das heisst, es muss einen Arbeitspunkt bestimmt werden, wonach sich die Eingangsspannung bezieht. Will man dabei erreichen, dass die maximale Eingangsspannung (nichtinvertierend, Verstärkung = 1) und die maximale Ausgangsspannung einigermassen symmetrisch sein soll, muss diese Arbeitspunktspannung in der Mitte zwischen +Ub und -Ub liegen, und das ist der GND. Man verwendet also den GND, der ein Netzteil mit ±Ub liefert. Vollständigkeitshalber sei aber erwähnt, dass es Anwendungen gibt, bei denen eine nichtsymmetrische Referenzierung sinnvoll ist, z.B. +12 VDC, GND und -6 VDC.

Einigermassen symmetrisch bedeutet, dass Opamp-Endstufen mit bipolaren Transistoren meist nicht symmetrisch aussteuerbar sind. Oft wird die positive Betriebsspannung schlechter approximiert als die negative. Oder anders erklärt: Wenn man mit einer Sinusspannung den Opamp allmählich aussteuert, wird meist zuerst die positive und, bei weiterem Anstieg der Spannung am Eingang, danach die negative Spannungsbegrenzung erreicht. Noch besser als mit einem Sinussignal erkennt man dieses Clipping mit einem Dreieicksignal an den Spitzen, wobei ein Dreiecksignal zusätzlich leichter erkennen lässt, ob es in der Nähe des Limits zu linearen bereits geringfügigen Verzerrungen (z.B. Slewrate-Effekte) kommt. Damit man eine symmetrische Signalbegrenzung bekommt, muss die Referenzspannung nicht mit GND, sondern mit einer DC-Spannung erzeugt werden, die die Ausgangssymmetrie herbeiführt. Dafür benötigt man ein RPR-Netzwerk, wie dies die Bilder 2 und 5 illustrieren.

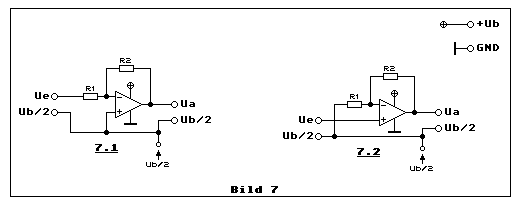
Bild 7 zeigt die invertierende und nichtinvertierende Verstärkerschaltung mit nur einer Betriebsspannung +Ub (Single-Supply). Dies bedeutet, dass die Referenz-, bzw. Arbeitspunktspannung "künstlich" realisiert sein muss. Wie man dies sinnvoll macht, wird weiter unten beschrieben. Mit dieser Methode hat man je nach dem, ob der GND dieser Schaltung mit dem GND weiterer Schaltungen (eines andern Gerätes) in Verbindung gebracht werden muss, ernsthafte DC-Offsetprobleme. Allerdings nur dann wenn DC-Spannungen (mit-)verstärkt werden müssen.

Ub/2 ist nicht die richtige Wahl, wenn die Aussteuerbarkeit des Opamps nicht symmetrisch ist. In diesem Fall muss man die Referenzspannung entsprechend anpassen. Deshalb liest man in den folgenden Bildern Ub/2 oder Ur (r=Referenz) oder beides, weil die Wahl des Opamps frei ist. Ein Rail-to-rail-Opamp erlaubt als Referenzspannung Ub/2.

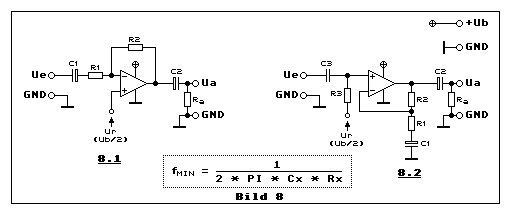
Bild 8 illustriert die invertierende und nichtinvertierende Verstärkerschaltung mit nur einer Betriebsspannung +Ub (Single-supply), welche jedoch nur AC-Spannungen verstärken. Die ein- und ausgangsseitigen passiven Hochpassfilter ermöglichen die einfache Anpassung an die externen Quellen und Empfänger. Man muss keine DC-Potenziale berücksichtigen. Teilbild 8.2 hat noch ein zusätzliches Hochpassfilter mit R1 und C1. Wozu das nötig ist, wird sogleich thematisiert.

Teilbild 8.1 illustriert den AC-gekoppelten invertierenden Verstärker. Er kann nur AC-Spannungen verstärken! Am nichtinvertierenden Eingang wird z.B. die halbe Betriebsspannung Ub/2 referenziert. Die AC-Spannungsquelle an Ue muss wesentlich niederohmiger als R1 sein, weil R1, wie wir jetzt wissen, den Eingangswiderstand der Verstärkerschaltung definiert. Ein zu hoher Innenwiderstand der AC-Quelle würde die Verstärkung reduzieren. C1 und R1 wirken als passives Hochpassfilter erster Ordnung. Dieses Hochpassfilter verhindert einerseits die Einkopplung von DC-Spannungsanteilen an Ue und es verhindert die Verstärkung von DC-Offsetspannungen die der Opamp selbst erzeugt. C1 ladet sich auf den Wert von Ur (Ub/2) auf, wenn die externe Spannungsquelle an Ue frei ist von einer DC-Offsetspannung. Sonst addiert sich die externe DC-Offsetspannung mit Ur. R2 existiert für die Berechnung von fmin nicht, weil R2 jenseits der extrem niederohmigen virtuellen Spannung am invertierenden Eingang liegt. R2 beeinflusst daher fmin nicht. Betreffs Formel zur Berechnung der Grenzfrequenz des Hochpassfilters ist Cx hier C1 und Rx hier R1 zuständig.

Es gibt aber nicht nur dieses Hochpassfilter, das die minimale Frequenz im Durchlassbereich von Ue zur Verstärkerschaltung bestimmt. C2 bildet mit dem Eingangswiderstand der folgenden Schaltung ein Hochpassfilter mit ebenfalls einer unteren Grenzfrequenz. Will man gar nicht erst den vielleicht schlecht definierten Eingangswiderstand der nachfolgenden Schaltung mit einbeziehen, setzt man selbst Ra zwischen Ua und GND, der signifikant niederohmiger sein sollte. Nun sollte man darauf achten, dass diese beiden passiven Hochpassfilter nicht dafür sorgen, dass die Amplitude in einem breiten unteren Nutzfrequenzbereich zu stark abfällt. Dieser Fall tritt nämlich dann ein, wenn die beiden -3dB-Grenzfrequenzen etwa identisch dimensioniert sind. Ich empfehle mit R1 und C1 die Grenzfrequenz zu dimensionieren, die man wirklich haben möchte. Für einen hochwertigen Audioverstärker z.B. bei 20 Hz oder weniger. Mit C2 und Ra wählt man eine drastisch niedrigere Grenzfrequenz. Diese darf durchaus bei 1 oder 2 Hz liegen. Es geht hier hauptsächlich nur darum, dass keine DC-Spannung mitverstärkt und übertragen wird.

Teilbild 8.2 zeigt den AC-gekoppelten nichtinvertierenden Verstärker. Am nichtinvertierenden Eingang wird über R3 ebenfalls z.B. auf die halbe Betriebsspannung Ub/2 referenziert. Ur (Ub/2) muss so niederohmig dimensioniert sein, dass R3 alleine die Grösse des Eingangswiderstandes bestimmt. Wie wir bereits wissen, ist ein JFET- oder MOSFET-Opamp extrem hochohmig. Also darf, je nach Anwendung, R3 auch sehr hochohmig gewählt werden. Allerdings sollte man nicht so sehr übertreiben, dass parasitäre Effekte, wie Widerstandsveränderung durch Umwelteinflüsse (bereits geringste Feuchtigkeit), sich bemerkbar machen. Man könnte z.B. für R3 100 M-Ohm und für C3 100 pF einsetzen, um eine untere Grenzfrequenz von 16 Hz zu erhalten. Dies wäre aber totaler Unsinn, wenn an Ue z.B. eine Audioquelle mit einem Quellwiderstand von 10 k-Ohm oder auch etwas mehr angeschlossen wird. Dazu genügt es wenn R3 auf maximal 1 M-Ohm festlegt wird. Mit C3 = 10 nF liegt dann die untere Grenzfrequenz dieses passiven Hochpassfilters ebenfalls bei 16 Hz.

Um Piezoeffekte möglichst zu vermeiden, sollte man für C3 ein Wickelkondensator dem Kerko unbedingt vorziehen. Für besonders niedrige untere Hochpass-Grenzfrequenzen, wo oft höhere Kapazitäten benötigt werden, kann man auch Elkos einsetzen, wobei man dafür vorzugsweise Tantalelkos oder Alu-Elkos mit speziell niedrigem Reststrom verwenden sollte. Es sei generell erwähnt, dass wegen diesem Piezoeffekt in emfindlichen Signalübertragungen keine Kerkos eingesetzt werden sollen, wohl aber zum Abblocken von Betriebsspannungen in der Nähe von empfindlichen Schaltungen (ICs)! Siehe Kapitel "Was ist der Piezoeffekt".

C3 und R3 bestimmen die eine untere Grenzfrequenz, C2 mit Ra eine andere, die, wie wir jetzt wissen, wesentlich niedriger sein sollte, als die von C3 und R3. Aber es gibt hier noch eine dritte untere Grenzfrequenz, diejenige welche durch das passive Hochpassfilter mit R1 und C1 bestimmt wird. Dieses Hochpassfilter verhindert, wie bei der Schaltung in Teilbild 8.1, die Verstärkung der DC-Offsetspannung des Opamp. C1 ladet sich auf den Wert von Ur (Ub/2) auf. Eine allfällige DC-Offsetspannung an Ue wirkt sich nicht aus, weil an C3 liegt. Man kann auf C1 verzichten und R1 direkt mit Ur (Ub/2) verbinden, wenn die Verstärkung des Opamp nicht eine unerträglich hohe DC-Offsetpannung an seinem Ausgang erzeugt, die hier aus der Verstärkung der opamp-internen DC-Offsetspannung entsteht. Es kommt ganz darauf an wie hoch die so genannte äquivalente DC-Offseteingangsspannung des Opamps und die gegengekoppelte Verstärkung ist. Unter äquivalent versteht man, dass es den selben Effekt hat, als ob der Opamp selbst keine DC-Offsetspannung erzeugt, die entsprechende DC-Spannung jedoch an einen Eingang gelegt wird. Für das Verstärkungsverhalten des Opamps kommt beides auf das selbe heraus. Bitte zu diesem Thema auch ein Opamp-Datenblatt studieren.

Man kann wählen ob man R1*C1 oder R3*C3 als dominierendes Hochpassfilter dimensionieren möchte. Wählt man R3*C3 für die erwünschte Grenzfrequenz, ist sichergestellt, dass das Eingangssignal bei einer Frequenz, welche um Grössenordnungen niedriger ist als die R3*C3-Grenzfrequenz, kaum noch auf den nichtinvertierend Eingang wirkt. Wählt man jedoch R1*C1 für die erwünschte Grenzfrequenz und die Grenzfrequenz von R3*C3 ist wesentlich niedriger, ist es so, dass nur eine Frequenz weit unterhalb dieser Grenzfrequenz nicht mehr übertragen werden kann. Aus der Sicht des R1*C1-Hochpassfilters, kann die Verstärkung nicht kleiner als 1 werden. Dies ist dann der Fall, wenn die Reaktanz (kapazitiver Widerstand) von C1 so hoch ist, dass C1 mit R1 und R2 nicht mehr als signifikanter Spannungsteiler wirkt. Man hat in diesem Zustand einen Spannungsfolger, weil es nur noch eine leitende Verbindung vom Opampausgang über R2 zum invertierenden Eingang gibt. Man beachte, in Bild 8 wird für die Kondensatoren, das Symbol des Elektrolytkondensators verwendet. Der Elko ist hier zulässig, weil die richtige Polarität der DC-Spannung gewährleistet werden kann. Eine Ausnahme bildet C3, weil R3 relativ hochohmig gewählt werden kann.

5.   Die Ub/2-Referenz und der synthetische GND

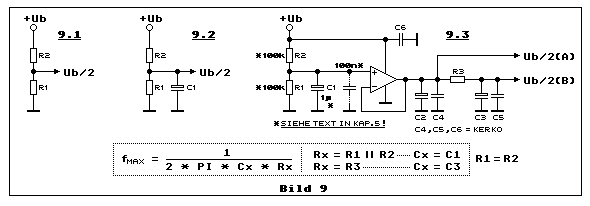
Bild 9 illustriert drei Beispiele wie die Referenzspannung Ub/2 realisiert werden kann. Das einfachste Beispiel ist ein Spannungsteiler mit zwei gleich grossen Widerständen R1=R2 (Teilbild 9.1). Der Quellwiderstand dieser einfachen Schaltung ergibt sich durch die Berechnung der Parallelschaltung von R1 mit R2. Wie wir bereits wissen, muss dieser Quellwiderstand möglichst niederohmig sein, wenn eine Verbindung zu einem Gegenkopplungsnetzwerk einer Opampschaltung besteht, damit die Verstärkung der Opampschaltung durch den Quellwiderstand dieser Ub/2-Quelle nicht signifikant beeinflusst wird. Für Teilbild 7.2 gilt, dass der Ub/2-Quellwiderstand stets wesentlich niederohmiger sein muss als der Eingangswiderstand der angeschlossenen Schaltung. Der Eingangswiderstand dieser Schaltung entspricht exakt dem Wert von R1.

Wesentlich unkritischer ist es, wenn nur AC-Spannungen oberhalb einer minimalen Frequenz verstärkt werden. Dann könnte man durchaus diese einfache Ub/2-Schaltung in Teilbild 9.2 verwenden, wenn parallel zu R1 ein Kondensator C1 geschaltet wird. Dieser sorgt dann oberhalb der minimalen Grenzfrequenz für eine entsprechend niedrige Quellimpedanz des R1||R2*C1-Netzwerkes. Man beachte, dass in diesem Fall nicht mehr von Quellwiderstand, sondern von Quellimpedanz die Rede ist. Es handelt sich um einen komplexen Widerstand. Die Grenzfrequenz des passiven R1||R2*C1-Tiefpassfilter sollte wesentlich niederfrequenter dimensioniert sein, als die untere Grenzfrequenz der involvierten Verstärkerschaltung! Diese Überlegungen gelten nur, wenn Ub/2 von Teilbild 9.2 DC-mässig praktisch unbelastet bleibt!
R1||R2*C1 bedeutet: R1 mit R2 erzeugt einen Parallelwiderstandswert und dieser bildet mit C1 einen komplexen Widerstand, eine Impedanz. Je höher die Frequenz um so niederohmiger die Impedanz.

Besonders dann, wenn eine Ub/2-Referenzspannung an vielen Stellen in einer Schaltung als Referenz dient und auch etwas belastet wird, eignet sich die Lösung mit einem Opamp, der mit Verstärkung 1 bloss als Impedanzwandler arbeitet, am besten. Dabei muss man berücksichtigen, dass eine Ausgangsstufe eines jeden Opamp rauscht. Problematisch ohne entsprechenden Filtermassnahmen ist dies, bei empfindlichen (Vor-)Verstärkern, wie z.B. für Mikrophone, Tonabnehmer, EMG, EKG oder EEG, falls diese Schaltungen mit +Ub (Single-Supply) gespeist werden und deshalb auf eine Referenzspannung angewiesen sind. Man betrachte dazu Teilbild 9.3. R1 und R2 arbeiten wiederum als Spannungsteiler, jedoch hat C1 hier eine etwas andere Funktion. Im Gegensatz zur passiven Schaltung, dürfen hier R1 und R2, besonders beim Einsatz von JFET- oder LinCMOS-Opamps (z.B. LF356, TL06x, TL07x, TLC271), hochohmig gewählt werden.

Extremwerte: Wenn es denn sein muss, mit je 10 M-Ohm. Theoretisch geht das tatsächlich, weil der maximale Input-Bias-Strom eines LinCMOS-Opamp des Types TLC271 beträgt gerade noch 60 pA bei 25 Grad Celsius. Typisch ist 0.1 pA. Ein Strom von 60 pA der durch einen Widerstand von 5 M-Ohm (beide 10M-Widerstände hier parallel gerechnet) fliesst, erzeugt eine Spannung von gerade mal 0.3 mV. Um diesen Spannungswert verändert sich am Knoten von R1 und R2 die Spannung nach oben oder nach unten. Die R1/R2-Knotenspannung beträgt bei einer Betriebsspannung +Ub von z.B. 5 VDC 2.5 VDC. Der Spannungsfehler der durch den Einsatz von 1%-Widerständen entsteht, beträgt maximal 50 mV und ist somit 170 mal grösser, als die Fehlerspannung verursacht durch den sehr niedrigen Biasstrom. Also ist der Fall klar, man darf für R1 und R2 je 10 M-Ohm oder auch höhere Werte einsetzen.

Stimmt das nun wirklich? In der Praxis natürlich nicht. Grundsätzlich gilt, je hochohmiger eine Schaltung konzipiert wird, um so störanfälliger ist sie. Es geht dabei längst nicht nur um elektrische Einflüsse. Bei derart hochohmigen Werten spielen bereits schwache Änderungen der Luftfeuchtigkeitswerte in der Umgebung eine Rolle. Auch sehr geringe Verschmutzung zwischen den Kontakten auf dem Print reduzieren signifikant solch hohe Widerstandswerte. Und damit würde sich die Referenzspannung drastisch ändern. Die Ausgangsspannung in einer Verstärkerschaltung würde asymmetrisch begrenzt, was die maximale Aussteuerung herabsetzt. Selbstverständlich kann man eine solch hochohmige Schaltung mit entsprechendem Aufbau und Einbau stabil arbeitend realisieren. Dies hier zu thematisieren würde jedoch den Rahmen sprengen.

Passend sind hier R1/R2-Werte (Teilbild 9.3) im unteren 100-k-Ohm-Bereich. C1 muss deshalb auch keinen hohen Kapazitätswert aufweisen. C1 unterdrückt Stör- und Rauschspannungen. Störspannungen entstehen durch parasitär kapazitive Einkopplung benachbarter AC-Spannungen (z.B. zwischen den Leiterbahnen) auf den Eingangsteil dieser Schaltung. Auch andere Schaltungsteile oder Geräte mit angeschlossenen Leitungen können stören. Dies soll C1 verhindern. Ist die Zeitkonstante von C1 mit R1||R2 (parallel) sehr gross, weil die Grenzfrequenz sehr niedrig gewählt ist, dauert es beim Einschalten der Betriebsspannung +Ub lange bis sich die Referenzspannung auf Ub/2 eingestellt hat. An so etwas ist bei der Schaltungsdimensionierung unbedingt auch zu denken!

Dazu eine kleine Überlegung bei R1 = R2 = 100-kOhm. Für C1 wählen wir 1 µF, ein Tantal-Elko, weil dieser Elko besonders verlustarm ist. Die Grenzfrequenz des passiven R1||R2*C1-Tiefpassfilter beträgt 3.2 Hz und die Ladezeitkonstante 50 ms. Das bedeutet, das eine Viertelsekunde (5-fache Zeitkonstante) nach dem Einschalten die Ub/2-Spannung praktisch erreicht ist. Die Grenzfrequenz ist niedrig genug um parasitär einkoppelnde niederfrequente Störspannungen ausreichend zu dämpfen. Die Bandbreite und damit die Rauschspannung selbst, am Eingang, ist ebenfalls drastisch reduziert. Will man eingangseitig auch höherfrequente Störspannungen berücksichtigen, empfiehlt sich parallel zu C1 noch einen Kerko mit 100 nF schalten. Dieser kompensiert eventuell parasitär induktive Anteile.

C1 hat keinen direkten Einfluss auf die Schaltung, welche an Ub/2(A) oder Ub/2(B) angeschlossen wird, wie dies im Sinne der passiven Schaltung (Teilbilder 9.1 und 9.2) der Fall ist. Wozu aber C2 am Ausgang des Opamps, der doch wegen der starken Gegenkopplung besonders niederohmig sein soll? Niederohmig ist er schon, aber nicht niederimpedant. Ich erinnere daran, dass bei höheren Frequenzen die Leerlaufverstärkung eines Opamp, wegen seiner (internen) Frequenzgangkompensation, abnimmt. Diese Abnahme hat zur Folge, dass der Ausgangswiderstand ansteigt (Verschlechterung der Regeleigenschaft) und dies kann sich ungünstig auf die gesamte Schaltung auswirken, wenn höhere Signalfrequenzen mit im Spiel sind. C2, ein Elko mit einem Wert von 10 µF bis etwa 100 µF am Ausgang des Opamp, stellt eine niedrige Impedanz von niederen bis mittelhohen Frequenzen sicher. Ein zusätzlich parallel geschalteter Kerko von etwa 100 nF (C4) senkt die Quellimpedanz zusätzlich für höhere Frequenzen. Will man zusätzlich niederfrequentes Rauschen des Opamp reduzieren, empfiehlt sich am Ausgang des Opamp ein zusätzlich niederimpedantes passives Tiefpassfilter mit R3, C3 und C5. R3 von wenigen zehn bis wenigen 100 Ohm und C3 im unteren 100 µF-Bereich, und parallel dazu ebenso ein Kerko mit einer Kapazität von 100 nF (C5).

Das Ansteigen des Ausgangswiderstandes bei zunehmender Frequenz ist das typische Verhalten einer Induktivität. Wir haben es hier mit einer aktiven parasitären Induktivität zu tun. Man merke sich dies, weil, wenn man den Ausgang des Opamps kapazitiv zu wenig belastet, kann das Eigenrauschen des Opamps bei einer gewissen Resonanzfrequenz einen überhöhten Wert annehmen. Ein Resonanzeffekt. Genau das selbe Problem hat man auch mit Spannungsregler-Schaltungen. Auch diese enthalten Verstärker. Tiefer mit diesem Thema befasst sich mein Elektronik-Minikurs Ein DC-Spannungsregler ist auch eine Induktivität!.

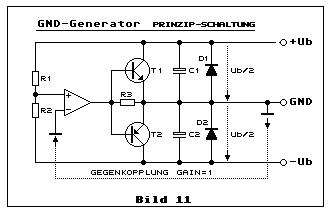
Dieser GND-Generator eignet sich dann, wenn keine symmetrische Betriebsspannung, bestehend aus ±Ub und GND, zur Verfügung steht. Ein GND der durch die angeschlossene Schaltung belastbar sein muss, also entsprechend grosse Ströme verarbeiten kann. Bild 11 ist nur eine Prinzipschaltung, wie sie im Buch Halbleiterschaltungstechnik von Tietze/Schenk im Kapitel "Symmetrische Aufteilung einer erdfreien Spannung" gezeigt und dort beschrieben wird. Wenn man diese Schaltung für die entsprechende Anwendung, speziell auf den Stromverbrauch, richtig dimensioniert - es können auch Darlington-Transistoren eingesetzt werden - funktioniert sie sehr gut auch im Ampere-Bereich. Ich habe vor einigen Jahrzehnten ein Leistungs-GND-Generator in einem Projekt realisiert und erfolgreich eingesetzt. Die Unterlagen dazu existieren leider nicht mehr, sonst hätte ich sie hier wiedergegeben. Ich schliesse aber nicht aus, dass ich dieses Thema eines Tages praxisorientiert erweitere und hier ergänze oder diesem Thema einen speziellen Elektronik-Minikurs widme. In diesem Fall wird dies im ELKO-Newsletter und auf der ELKO-Hauptseite bekanntgegeben.

6.   Der unbenutzte Opamp und die richtige Beschaltung

Es kommt bei einem Vierfach-Opamp (Quad-Opamp) immer wieder mal vor, dass man in einer Schaltung nur drei dieser vier Opamps benötigt und da stellt sich die Frage, wie man den unbenutzten Opamp richtig beschaltet.

Die Methode wie man mit unbenutzten Eingängen von Logikgattern (Teilbild 12.1) richtig umgeht, auf unbenutzte Eingänge von Operationsverstärkern (Teilbilder 12.2 und 12.3) überträgt, ist absolut unzulässig und doch sieht man immer wieder Schaltungen mit dieser Scheinlösung. Richtig ist es, dass die nicht benutzten Eingänge im zulässigen Gleichtaktbereich liegen müssen. Bei "normalen" Opamps ist das etwa zwischen +Ub-2V und -Ub+2V, bei Rail-to-rail-Opamps zwischen +Ub und -Ub und bei so genannten Single-Supply-Opamps (z.B. LM324, LM358, TLC271 bis TLC274) zwischen +Ub-2V und GND (Teilbild 12.3). Ob die beiden unbenutzten Eingänge offen oder an ein gemeinsames Potential innerhalb des Gleichtaktbereiches verlötet sind, beides ist unstabil. Da nicht gegengekoppelt, wirkt die extrem hohe innere Leerlaufverstärkung (Open-Loop-Gain) mit einem Faktor von einigen 10'000 bis mehr als 100'000 im DC-Bereich und bei sehr niedrigen Frequenzen zwischen etwa 10 und 100 Hz. Oberhalb sinkt die Leerlaufverstärkung um typisch 20 dB pro Frequenz-Dekade. Hier ein Beispiel zum JFET-Opamp TL071. Geringste Störspannungen an den Eingängen - auch wenn die gemeinsam auf dem selben Potential liegen (z.B. GND-Loops) - können zu grossen Spannungsschwankungen am Ausgang des Opamps führen, oft gleich bis in Grenzbereich, begrenzt durch die Betriebsspannung. Dies stört, je nach Anwendung, die benachbarten Opamps im selben IC. Auch die thermische Drift kann ein Auslöser von spontanen Spannungsänderungen am Ausgang sein.

Die Teilbilder 12.4 und 12.5 zeigen wie man es richtig macht. Man setzt den Opamp auf Verstärkung 1 und setzt den nichtinvertierenden Eingang auf ein beliebiges Potential innerhalb des zulässigen Gleichtaktbereiches. Passend ist im Dual-Supply-Mode (±Ub) stets der GND-Bezug. Im Single-Supply-Mode taugt ebenfalls der GND-Bezug, wenn der Opamp Single-Supply-fähig ist (Beispiele: LM324 und TLC274). Dies ist dann der Fall, wenn der Opamp eine Eingangsspannung bis hinunter auf das untere Potential der Betriebsspannung (-Ub oder GND) zulässt. In den Teilbildern 12.5 und 12.7 ist dies der GND. Ist der Opamp nicht Single-Supply-fähig, muss man den nichtinvertierenden Eingang mit einer Referenzspannung verbinden, die eine analoge Schaltung im Single-Supply-Mode oft benötigt (Kapitel "Die Ub/2-Referenz und der synthetische GND") oder man realisiert einen Spannungsteiler mit einem Abblockkondensator (R,R,C), wie dies Teilbild 12.5 zeigt.

Die Teilbilder 12.6 und 12.7 zeigen was zu tun ist, wenn der Opamp nicht Unity-Gain-stabil ist. In diesem Fall liest man im Datenblatt die Minimal-Verstärkung. Unterschreitet man diese, oszilliert der Opamp. Mit R1 und R2 wählt man eine Verstärkung die etwas grösser ist als die zulässige Minimal-Verstärkung. Da solche Opamps meist recht schnell sind, sollte man besonders darauf achten, dass die Verbindungen zum invertierten Eingang so kurz wie möglich sind.

6.1   Wenn Opamps andere Opamps stören

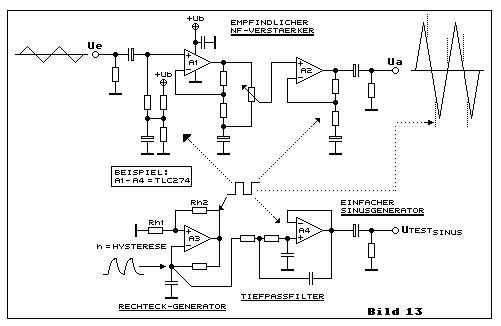
In einem Quad- oder auch Dual-Opamp kann man nicht alle Schaltfunktionen gemeinsam integrieren die man gerne haben möchte. So ist es z.B. nicht empfehlenswert eine empfindliche Verstärkerschaltung und ein Rechteckgenerator gemeinsam in einem IC unterzubringen, weil steile Flanken und hohe Amplituden die analoge Schaltung empfindlich stören können. Dies hat zur Folge, dass das Ausgangssignal Ua mit schmalen Impulsen überlagert ist oder das Signal verzerrt wird. Selbst dann wenn die zugehörigen passiven Bauteile nicht zu nahe beieinander liegen, erfolgt noch immer ein hohes Mass an Störung im Bereich des Chips. Für den NF-Verstärker kann man einen Dual-Opamp, z.B. den TLC272, einsetzen. Jedoch für den einfachen Sinusgenerator, bestehend aus Rechteckgenerator und aktivem Tiefpassfilter mit einer Festfrequenz, lohnt sich je ein Opamp zu verwenden, z.B. den TLC271. Diese Schaltung ist nur grad ein Beispiel um das Störphänomen zu erklären. Selbstverständlich kann man den Sinus-Testgenerator auch ganz anders realisieren.

Fazit: Man sollte keine analogen und (quasi-)digitalen Signale in einem Mehrfach-Opamp unterbringen, wenn Signalreinheit eine signifikante Rolle spielt. Man kennt dieses Problem z.B. bei integrierten SC-Tiefpassfiltern. Allerdings kennt man bei diesen Schaltungen die Verhältnisse. Das Verhältnis der Abtastfrequenz zur Grenzfrequenz ist gross und konstant. Dies macht es relativ einfach mit dem Problem des Clock-Feedthrough vernünftig umzugehen.

Bild 14 klärt auf, warum die Unity-Gain-Bandbreite nur für die Verstärkung von 1 (nichtinvertierend) und nicht auch für die Verstärkung von -1 (invertierend) gilt. Als Beispiel dient der Opamp LF356 mit einer Unity-Gain-Bandbreite von 5 MHz. Die Frequenzangaben in Klammern beim Ausgang Ua ist jeweils die resultierende Grenzfrequenz (-3dB). Die DC-Spannungswerte an Ue und Ua und über R1 und R2 dienen als Beispiele zum leichteren Verständnis betreffs der Verstärkung.

Teilbild 14.1 zeigt die vollständige Gegenkopplung durch die direkte Verbindung von Ua mit dem invertierenden Eingang. Auf diese Weise arbeitet der Opamp mit einer geschlossenen Schlaufenverstärkung (Closed-Loop-Gain) von 1 bis zur angegebenen Frequenz der Unity-Gain-Bandbreite (LF356 = 5 MHz). Die Grenzfrequenz ist identisch mit der Unity-Gain-Bandbreite.

Teilbild 14.2 zeigt die invertierende Verstärkerschaltung mit einer Verstärkung von -1, gegeben durch R1 = R2. Die Grenzfrequenz beträgt aber nur die die Hälfte der Unity-Gain-Bandbreite, also 2.5 MHz, weil die Gegenkopplung nur die Hälfte ausmacht. Der Knoten R1/R2 liefert zum invertierenden Eingang nur die halbe Spannung von Ua-Ue. Diese beträgt im Beispiel aus +1V plus -1V exakt 0V (virtueller GND-Pegel). Ob Ue an R1 liegt (Gain = -1) oder am nichtinvertierenden Eingang in Teilbild 14.3 (Gain = +2) spielt dabei keine Rolle. Die Schaltung benötigt überhaupt keine Eingangsspannung. Die Tatsache, dass die Grenzfrequenz der halben Unity-Gain-Bandbreite entspricht, ist alleine abhängig vom Gegenkopplungsnetzwerk.

Teilbild 14.4 zeigt nichts Neues im Vergleich zu Teilbild 14.3. Beide Schaltungen sind nichtinvertierende Verstärker. Der einige Unterschied besteht darin, dass in Teilbild 14.3 nur mit einem Faktor +2 und in Teilbild 14.4 mit +11 verstärkt wird, jeweils nachvollziehbar mit den DC-Spannungsangaben an Ue und Ua. Mit einer Verstärkung von 11 reduziert sich natürlich die Grenzfrequenz auf einen Wert von weniger als 0.5 MHz, berechnet nach der Formel:
( fg = fUGBW / GainClosed-Loop )

Es mag sich der eine oder andere Leser fragen, warum es denn zu R1 parallel R3 braucht, um auf einen Wert von 220 Ohm zu gelangen. Schliesslich gibt es Widerstände mit exakt 220 Ohm. Es genügt R1 = 220 Ohm und die Schaltung verstärkt korrekt mit +11. Diese Überlegung ist richtig, wenn da keine spezielle Absicht dahintersteckt, aber diese gibt es mit Teilbild 14.5 als invertierender Verstärker. Da gibt es den R3 gleich nochmals zwischen dem invertierenden Eingang und GND. Sogleich stellt sich die Frage nach dem Wozu, denn R3 verbindet den virtuellen mit dem echten GND. Kein Strom fliesst durch R3. Also ist das eine Witzschaltung?

Keinesfalls! Erstens fliesst ein sehr kleiner Strom durch R3 (die offene Schlaufenverstärkung ist nicht unendlich!), der für das richtige Funktionieren sogar wichtig ist und zweitens will ich damit etwas erklären. Obwohl von Ue nach Ua nur um einen Faktor -1 verstärkt wird, hat diese Schaltung nicht die selbe Grenzfrequenz wie Teilbild 14.2 zeigt. Es sind nur 0.5 MHz wie Teilbild 14.4 zeigt mit einer Verstärkung von +11. Einen praktischen Nutzen hat diese Schaltung in Teilbild 14.5 nicht. Eher das Gegenteil gibt es. Die nutzlose Schaltung (R3) reduziert die Grenzfrequenz und erhöht an Ua die äquivalente Eingangs-Rauschspannung des Opamp, weil diese wird wegen R3 (und R2) mit +11 verstärkt. Allerdings nicht mit dem Faktor der nutzlosen Verstärkung, weil durch die Reduktion der Grenzfrequenz die Rauschspannung reduziert wird. Diese beiden Antagonisten Verstärkung und Bandbreite kompensieren sich aber nicht, weil sich die Rauschspannung nur mit der Quadratwurzel der Frequenzänderung reduziert. Mehr dazu erfährt man, wenn man sich mit der so genannten Rauschspannungsdichte befasst. Dazu eignet sich der Elektronik-Minikurs Rauschdämpfung mit Tiefpassfilter. Es gibt allerdings einen praktischen Nutzen mit Teilbild 14.5. Wenn man einen Opamp einsetzen will, der die Verstärkung 1 nicht zulässt, weil er intern nur teilweise kompensiert ist, gibt es den Trick, dass man mit R2, R3 und C die nutzlose Verstärkung bei den höheren Frequenzen anhebt. Diese muss so hoch sein, dass die Phasenreserve gross genug bleibt, damit sicher kein instabiles Verhalten (Oszillation) erzeugt wird. So kann man mit einer Verstärkung, unterhalb der minimalen Verstärkung, gemäss Datenblatt, arbeiten und die, wegen R2/R3, erhöhte Rauschspannung macht sich innerhalb z.B. der Audio-Grenzfrequenz nicht nennenswert bemerkbar. Damit sinnvollerweise nur höhere Frequenzen von der nutzlosen Verstärkung betroffen sind, muss man in Serie zu R3 C schalten. Damit wird dieser höhere Frequenzanteil durch dieses R3*C-Hochpassfilter definiert. Eine solche Schaltung gibt es als Applicationnote mit Berechnungsformel im LF356-LF357-Datenblatt auf Seite 20 in Figure 52 und Figure 53. Der Kompromiss, den man dabei eingeht, besteht in der Reduktion der Grenzfrequenz, wie wir jetzt wissen.

Dieser Hinweis mit dem LF357 dient nur der Anschauung. Der LF357 wird schon seit vielen Jahren nicht mehr hergestellt, doch den LF356 dürfte es wahrscheinlich noch lange geben. Man beachte die grosse Vielfalt der Applicationnotes im Datenblatt. Trotzdem kann das Wissen dieses Tricks wertvoll sein, wenn man z.B. einen schnellen Quad-Opamp einsetzt, der intern nur teilkompensiert ist und nicht bis zur Verstärkung 1 benutzt werden kann. Jedoch einer dieser vier Opamps benötigt man für die Verstärkung von 1 als Impedanzwandler und die dadurch reduzierte Grenzfrequenz stört nicht. In diesem Fall käme Figure 52 zum Einsatz.

Teilbild 14.6 zeigt einen invertierenden Verstärker mit zwei Eingängen Ue1 und Ue2. Ue1 wird niedrig mit einem Faktor von -1 verstärkt und Ue2 wird höher mit einem Faktor von -10 verstärkt. Betreffs der Grenzfrequenz für beide Eingänge dominiert Ue2, falls Ue2 an eine niederohmige Quelle angeschlossen ist, mit den angegebenen 0.5 MHz (Teilbild 14.5). Wenn Ue2 offen und nur Ue1 in Betrieb ist, gilt die Grenzfrequenz von 2.5 MHz (Teilbild 14.2).

Opamps welche hier zur Anwendung kommen, dienen in der Regel für niederfrequente Anwendungen (z.B. Audio, Elektromyographie [EMG]). Die relativ hohe UGBW-Frequenz solcher Opamps ist hauptsächlich dann relevant, wenn hohe Verstärkungen zum Einsatz kommen. Warum, ist weiter oben ausführlich erklärt. Arbeitet eine Opamp-Schaltung jedoch als Impedanzwandler (Verstärkung = 1) oder sonst mit sehr niedriger Verstärkung, eignen sich diese Opamps, wie z.B. LF356, TL071 oder TLC271 (im High-Bias-Mode), durchaus für den Einsatz höherer Frequenzen, bis in den unteren bis maximal mittleren 100-kHz-Bereich. Man muss dabei auch die Slewrate, abhängig von der Ausgangsspannung, berücksichtigen, wie ebenfalls weiter oben ausführlich thematisiert.

Wir setzen an dieser Stelle fort mit den Schaltungen in Bild 14 und experimentieren. Diese Experimente werden sogleich zeigen, dass Simulationen als Alternative nicht geeignet sind, weil die Störeffekte, die sich durch den Versuchsaufbau ergeben, nicht simuliert werden können. Für solche Versuche eignen sich am Besten so genannte Experimentier-Steckboards. Aus diesem Link, zur weiteren Erklärung, das folgende Bild, eine Skizze des Experimentier-Boards gleich hier:

Es ist die selbe Skizze von der Hobby-Bastelecke. Die zusätzlichen Eintragungen 'Hobby-Bastelecke', '+Ub', 'GND' und '-Ub' sind von mir.

Hier sieht man zwei parallele Reihen von fünf senkrechten Steckbuchsen die boardintern miteinander verbunden sind von a bis e und von f bis j. Oben und unten hat es waagrecht angeordnete Steckbuchsen, ebenfalls in 5er-Gruppen. Es sind jedoch alle Buchsen in einer Zeile boardintern mit einander verbunden. Die roten Linien sind mit '+' und die blauen mit '-' gekennzeichnet.

Arbeitet die Testschaltung im Dual-Supply-Mode, also mit ±Ub, empfiehlt es die innen liegenden Steckzeilen '+' und '-' mit GND zu verbinden. Der praktische Vorteil ist der, dass GND-Verbindungen zur Testschaltung oft häufiger sind als die Plus- und Minus-Verbindungen. Die Verdrahtung mit Drahtbrücken ist so einfacher. Die Zeile mit +Ub (rote Linie) ist ganz oben und die Zeile mit -Ub (blaue Linie) ganz unten im Bild. Bild 15 zeigt eine praktische Anwendung:

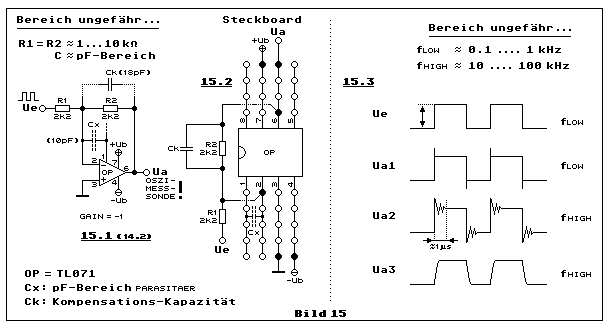
Die UGBW liegt beim TL071 bei 3 MHz anstatt 5 MHz wie beim LF356. Teilbild 15.1 zeigt die Schaltung aus Teilbild 14.2 und das heisst, man will testen, was es mit der Grenzfrequenz auf sich hat, die bei der Verstärkung von -1 (invertierend) nur halb so gross ist wie die Verstärkung von +1 (nichtinvertierend), auch als Spannungsfolger oder Impedanzwandler bezeichnet. Anstelle des Opamp LF356 kommt hier ein TL071 zum Einsatz. Beides sind JFET-Opamps, aber der TL071 (TL081) eignet sich speziell zum Zeigen eines unerwünschten Effektes, der auch bei andern Opamps auftreten kann, wenn vielleicht auch nicht in Zusammenhang mit den selben IC-Anschlüssen.

Oszi-Messonde: Warum wird dies gerade hier thematisert? Wenn man die Ausgangspannung einer Opampschaltung im höheren Frequenzbereich der UGBW auf dem Oszilloskopen beobachten will, dann beobachtet man kaum dies, was man zu sehen erwartet, weil der Schaltungsaufbau wegen pararasitären Kapazitäten dies verhindert. Bei besonders hochfrequenten Opamps, sind auch parasitäre Induktivitäten am Problem beteiligt. Man sollte auch daran denken, dass man mit einer niederkapazitiven Mess-Sonde an Ua misst, weil der direkte Anschluss einer Koaxialleitung, kann wegen zu hoher kapazitiven Last, die Schaltung leicht zum Oszillieren bringen oder es verzerrt zu mindest selbst zusätzlich die Ausgangsspannung.

Dieses Functional Block Diagramm des TL071 zeigt mit meinen roten Einträgen worum es geht. Der P-Kanal-JFET verstärkt die sehr kleine AC-Spannung am invertierenden Eingang auf den Drain (D) und von hier gelangt diese Spannung über den Kollektor zum Emitter von T1 auf den Widerstand mit einem Wert von 1080 Ohm. Diese Spannung N1 liegt an Pin 1. Nun weiss man, dass der invertierende Eingang des Opamp in seiner gegengekoppelten Verstärkerfunktion generell extrem sensibel ist. Das ist auch der Grund weshalb die Leiterbahn des invertierenden Eingangs grundsätzlich immer so kurz wie möglich sein sollte. Im vorliegenden Beispiel ist es die parasitäre Kapazität Cx, die sich aus dem Abstand der beiden Leiterbahnen von Pin 1 und Pin 2 und aus der gemeinsamen Länge ergibt. Cx bewirkt, abhängig von der Signalfrequenz, einen Mitkopplungseffekt. Dies hat als Störung nichtlineare Effekte an Ua zur Folge, die im weiteren Verlauf thematisiert sind.

Zurück zu Teilbild 15.1. Die Werte von R1 und R2 mit je 2.2 k-Ohm sind für dieses Experiment relativ niederohmig gewählt. Dies hat den Grund, damit man mit der Signalfrequenz an Ue möglichst weit hochfahren kann, ohne dass es zu Signalverzerrungen (nichtlineare Effekte) kommt. Im Test bauen wir jedoch einen Kerko von 10 pF (Cx) ein. Darum ist Cx gestrichelt gezeichnet. Dies soll andeuten, Cx existiert auch ohne den Einsatz eines Kondensators, wie bereits beschrieben. Die reale Kapazität Cx ist durch den Versuchsaufbau um einige pF höher. Wenn es zu einer erkennbaren Beeinfluss durch Cx kommt bei den hohen Frequenzen, erkennt man dies auch schon mit einer steilfankigen Rechtechspannung Ue mit niedriger Frequenz im unteren kHz-Bereich, wie dies Ua1 in Teilbild 15.3 zeigt. Man sieht ein sauberes Rechtecksignal, jedoch bei den steilen Schaltflanken erkennt man feine Peaks. Dehnt man auf dem Oszilloskop diese Peaks im Zeitbereich, zeigen sie sich als gedämpfte Schwingungen, dargestellt mit Ua2. Die Erhöhung der Rechteckfrequenz führt zum selben Effekt, weil die Details der gedämpften Schwingung ist nur von der Flankensteilheit und nicht durch die Frequenz der Rechteckspannung bedingt.

Dieses Einschwingen in der Form einer gedämpften Schwingung, lässt sich mit einer Kapazität von Ck = 18 pF auf praktisch Null reduzieren, so wie dies das Diagramm Ua3 zeigt. Bei eigenen Experimenten können die Resultate von den Angaben hier abweichen, weil der Aufbau jeweils unterschiedlich ist. Das spielt aber keine Rolle, weil es nur darum geht ein Störfall zu illustrieren, um daraus das Grundsätzliche praxisnah zu erlernen.

Teilbild 15.2 skizziert die Anordnung von R1, R2 und Ck vom Ausgang Pin 6 zum invertierenden Eingang Pin 2. Pin 1 und Pin 5 dienen dem DC-Offsetabgleich mittels Trimmpot, falls dies nötig ist. Unabhängig davon beeinflusst die Signalspannung an Pin 1 den invertierenden Eingang, vor allem bei höheren Frequenzen, weil da die Kapazitanz von der parasitären Kapazität Cx deutlich höher ist. Bei einem Rechtecksignal betrifft dies die höheren Frequenzanteile, erzeugt durch die steilen oberwellenreichen Schaltflanken. Mit einem Radio mit Mittelwellenempfang in der Nähe der Experimentierschaltung kann man die niederfrequente Frequenz der Rechteckspannung hören, weil der Empfänger die Oberwellen mit Frequenzanteilen bis in den MHz-Bereich amplituden-demoduliert. Ich empfehle, einfach ausprobieren.

Bild 16 illustriert noch einmal das Resultat im Zeitbereich, so wie es in Bild 15 dargestellt ist, und hier zusätzlich das Resultat im Frequenzbereich, jeweils an Ua. Für die Darstellung im Zeitbereich eignet sich eine Rechteckspannung mit einer (fixen) Frequenz und für die Darstellung im Frequenzbereich mit einer variablen Sinusspannung. fix in Klammer bedeutet, dass eine fixe Frequenz genügt, sie darf ebenfalls auch variabel sein. Dies, weil die aperiodische Schwingung nur durch die Flankensteilheit und nicht durch die Frequenz bedingt ist.

Teilbild 16.1 wiederholt Teilbild 15.1. Zunächst fehlt Ck mit 18 pF, Cx als zugefügter Kondensator soll 10 pF haben. Genau wie zuvor in Bild 15. Teilbild 16.2a wiederholt Ua von Teilbild 15.3-Ua2 mit der aperiodischen Schwingung. Solange das Verhältnis T/d gross ist, wirkt sich dies im Frequenzgang kaum aus. Das bedeutet, wenn man an Ue anstelle der oberwellenreichen Rechteckspannung eine Sinusspannung anlegt, hat man einen einen relativ grossen Frequenzbereich, bei der die Ausgangsspannung Ua konstant bleibt. Im vorliegenden Beispiel mit der Verstärkung von -1, dargestellt in Teilbild 16.2b. Je höher die Sinusfrequenz eingestellt wird, um so grösser wird die Spannungsabweichung. Sie beginnt bei etwa 0.5 MHz, erreicht ein Maximum bei etwa 1.3 MHz, fällt danach wieder und erreicht bei etwa 2.5 Mhz die typische -3dB-Grenze. Dies entspricht der UGBW. Damit dies einigermassen zutrifft, muss man mit Cx etwas experimentieren.

Fügt man die Kompensations-Kapazität Ck von 18 pF (auch hier etwas experimentieren!) ein, dann wird die aperiodische Schwingung so weit gedämpft, wie dies Teilbild 16.3a (15.3-Ua3) im Zeitbereich zeigt. Die Rechteckspannung an Ue wird mit leicht reduzierter Flankensteilheit nach Ua übertragen. Dies hat zur Folge, dass eine Sinusspannung an Ue sich im Frequenzbereich linear verhält. Erst dann wenn an Ue die Sinusfrequenz hoch genug ist, verhält sich die Ausgangsspanng an Ua nichtlinear. Ck dämpft so stark, dass es im Nahbereich der Grenzfrequenz keine Spannungserhöhung gibt. Oberhalb von etwa 1.5 MHz sinkt die Amplitude ebenfalls auf die selbe -3dB-Grenzfrequenz von etwa 2.5 MHz.

Praktische Übung und Erkenntnis: Ich empfehle mit dieser Versuchsschaltung selbst mit einem Experimentierboard zu üben. Die gemessenen Werte können von den Angaben je nach Art des Aufbaus abweichen. Darum die Experimentierempfehlung.

Welchen Nutzen hat diese Übung? Man erkennt welche dynamische Auswirkung es hat, wenn R1 und R2 höher als diese 2.2 k-Ohm gewählt werden. Sind es z.B 22 k-Ohm, dann hat eine parasitäre Cx-Kapazität die selbe Auswirkung, wenn sie nur 1 pF beträgt. Das ist eine solch kleine Kapazität die nur schon durch zwei benachbarte sehr kurze Leiterbahnen entstehen. Das bedeutet, man ist dieser Realität ausgeliefert. Wohlverstanden bei der höheren Frequenz im oberen 100-kOhm-Bereich und mehr, jedoch nicht in der niederfrequenten Region des Audio oder z.B. Elektromyographie. Auch hier, unbedingt mit unterschiedlichen R1=R2-Werten experimentieren. Daraus lernt man, dass eine Verstärkerschaltung so niederohmig wie realistisch möglich dimensioniert werden soll. Und dies längst nicht nur wegen diesem Störeffekt. Man reduziert damit auch die Störsensibilität bezüglich externen Störquellen.

R2 ist eine Last: Man kann R2 nicht beliebig reduzieren, weil sonst die Opamp-Endstufe überlastet wird. Beim TL071 gilt ein Minimalwert von 2 k-Ohm, der in vielen Diagrammen zum Ausdruck kommt. Besonders betroffen ist die Aussteuerbarkeit der Ausgangsspannung, wenn man diese 2 k-Ohm deutlich unterschreitet. Es gilt dabei eine Betriebsspannung von ±15 VDC. Es gibt moderne Opamps die eine bessere Treiberfähigkeit haben. Schon der alte NE5534 vermag bei ±15 VDC einen Lastwiderstand von 600 Ohm mit einer Aussteuerbarkeit von 20 Vpp (pp = Sinus peak-to-peak) treiben.

Block-/Stütz-Kondensatoren: In den Schaltbildern nicht gezeichnet sind Kerko mit einer Kapazität von typisch 100 nF zwischen +Ub und GND und -Ub und GND direkt bei den Opamps. Am Eingang des Experimentierboards empfiehlt sich je ein Elko mit 10 bis 100 µF ebenfalls zwischen +Ub und GND und -Ub und GND. Diese Massnahmen unterstützen die Funktionsstabilität. Vor allem die Kerko sind wichtig!

Fourier-Transformation: Vollständigkeitshalber sei hier noch erwähnt, dass der Zusammenhang der aperiodischen Dämpfung im Zeitbereich und das Spektrum im Frequenzbereich, wie hier als praktisches Beispiel beschrieben, in der Mathematik der Fourier-Transformation ihre theoretische Basis hat. Falls in diesem wissenschaftlichen Bereich Fragen "auftauchen", bin ich leider nicht der geeignete Ansprechpartner darauf zu antworten. Sorry.

Es gibt den piezoelektrischen Sensor. Bei Belastung durch Zug-, Druck- oder Schubkräfte wird eine elektrische Ladungsverschiebung und dadurch eine elektrische Spannung erzeugt. Diese Spannung tritt aber nur relativ kurzzeitig, während einer Kraftänderung in Erscheinung. Angewendet wird dies auch in einem Gasfeuerzeug mit elektrischem Hochspannungsfunken. Dieser wird durch einen kurzzeitigen mechanischen Schlag auf ein piezosensitives Teil erzeugt. Das selbe passiert - wenn auch nur Spannungen im mV- bis in den 10-mV-Bereich - wenn man mit einem harten Gegenstand auch nur leicht einen keramischen Kondensator beklopft. Den selben Effekt kann man feststellen, wenn man ein abgeschirmtes Kabel an einem empfindlichen Mikrofoneingang anschliesst und das relativ niederohmige Mikrofon nicht angeschlossen ist. Man hört es aus dem Lautsprecher problemlos, wenn man an das abgeschirmte Kabel klopft. Auch das ist eine Art Piezoeffekt. Der mechanische Impuls erzeugt kurzzeitige Ladungsverschiebungen in der Isolation zwischen Innenleiter und Abschirmung. Zu diesem Thema empfehle ich Im Fokus: Der Piezo-Effekt.

• Operationsverstärker II: Die Gain- und die Offsetabstimmung, und die Problembeseitigung von kapazitiver Belastung am Ausgang des Operationsverstärkers, die so genannte Lead-Kompensation.


• Operationsverstärker III: Vertiefung zum Thema virtuelle Spannung/GND. Ein etwas anderer Erklärungsansatz, ein Versuch zum leichteren Verständnis...


• Vom Operationsverstärker bis zum Schmitt-Trigger, kontinuierlich einstellbar. Eine Demoschaltung! Vor allem geeignet für Lehrer, welche Elektronik-Azubis ausbilden!


• Echter Differenzverstärker I: Die Überlegenheit des Instrumentationsverstärkers gegenüber dem Operationsverstärker. Elektromedizinische Hinweise wie EMG und EKG.


• Echter Differenzverstärker II: Referenzierung betreffs Spannungsmessung und DC-Offsetspannung.


• Echter Differenzverstärker III: Analysieren und Verstehen des Instrumentationsverstärkers.


• Echter Differenzverstärker IV - EMG-Vorverstärker Deluxe mit INA111: Beachte auch speziell das Kapitel "Erste Stufe stärker als die zweite"


• Rauschdämpfung mit Tiefpassfilter


• Ein DC-Spannungsregler ist auch eine Induktivität! Und das selbe gilt auch für "nur" einen gegengekoppelten Verstärker...


• What's All This Slewrate Stuff, Anyhow?
  Eingabe: Frequenz-Bandbreite, Amplitude
  Resultat: Slewrate

Thomas Schaerer, 26.06.2002 ; 13.11.2002 ; 16.12.2002 ; 15.04.2003(dasELKO) ; 16.12.2003 ; 30.12.2004 ; 15.11.2005 ; 12.05.2007 ; 15.06.2010 ; 25.12.2010 ; 27.06.2011 ; 08.01.2012 ; 13.03.2012 ; 05.09.2013 ; 26.03.2014 ; 07.02.2016 ; 23.04.2017