Ein DC-Spannungsregler ist auch eine Induktivität!
- Elektronik-Minikurse: Inhaltsverzeichnis WICHTIG: Diverse technische Infos
- Elektronik-Minikurse: Philosophie (Sinn, Vorwissen, Praxisbezug)
- Hilfe bei Leserfragen. (WICHTIG: Unbedingt zur Kenntnis nehmen!)
- Simulieren und Experimentieren, ein Vorwort von Jochen Zilg
- Autor: Thomas Schaerer Opamp-Buch Timer555-Buch
Einleitung
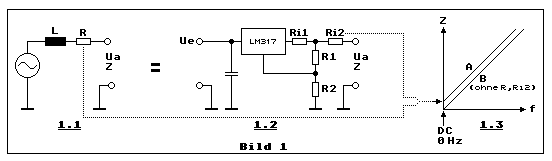
Nein, Bild 1 ist kein Irrtum und der Leser wird auch nicht über den
Tisch gezogen. Es ist bloss eine Frage der Betrachtung, und die
Gleichsetzung von einer Wechselspannungsquelle mit einem
induktiv-komplexen Widerstand (Teilbild 1.1) mit einer
DC-Spannungsreglerschaltung (Teilbild 1.2) ist zulässig. Es geht also um
die Behauptung, dass ein DC-Spannungsregler auch eine induktiv-komplexe
Eigenschaft hat. Dieser Behauptung wollen wir hier Schritt für Schritt
nachgehen. Mit induktiv-komplex ist die reale induktive Einheit gemeint,
die aus einem induktiven frequenzabhängigen Widerstand und einem
seriellen parasitären ohmschen Widerstand besteht. Weitere eher
nebensächlichere parasitäre Effekte des Spannungsreglers interessieren
uns hier nicht. Der induktiv-komplexe Widerstand nennt man Impedanz.
Das Diagramm in Teilbild 1.3 zeigt die Zunahme der Impedanz Z in
Funktion der Frequenz f mit zwei idealisierten Kurven A und B. Kurve A
illustriert das Verhalten von Teilbild 1.1 mit dem ohmschen
Verlustwiderstand R in Serie zu L, jedoch ebenso das Verhalten von
Teilbild 1.2, wenn der Innenwiderstand Ri2 (Leitungswiderstand)
berücksichtigt ist. Für beide Schaltungen gilt: Z ist abhängig von f.
Ist f = 0 Hz, dann gibt es keinen induktiven Widerstand, jedoch der
Verlustwiderstand, also R (Teilbild 1.1) und Ri2 (Teilbild 1.2), bleibt
natürlich erhalten. Darum geht die Kurve A nicht auf 0 Ohm, wenn f = 0
Hz. In der DC-Reglerschaltung von Teilbild 1.2 gibt es auch noch den
Innenwiderstand Ri1 innerhalb der Regelschlaufe. Dieser Widerstand wird
durch die Schaltung auf einen sehr niederohmigen Wert ausgeregelt (Kurve
B), ausser wenn an Ua höhere Schaltgeschwindigkeiten oder an Ue höhere
Frequenzen von Spannungsänderungen (z.B. mittel- bis hochfrequente
Rippelspannungen) wirksam sind. Ri1 verhindert also keineswegs, dass der
Innenwiderstand (Innen-Impedanz) des DC-Spannungsregler statisch
praktisch 0 Ohm haben kann. Ri1 kann parasitär, allerdings z.B. auch ein
Strommess-Shuntwiderstand sein. Für die Kurve B bleiben R und Ri2
unberücksichtigt.
Jeder DC-Spannungsregler enthält einen Regelverstärker und darum kann
man die Erkenntnis, dass ein DC-Spannungsregler auch eine Induktivität
ist, auf eine simple Verstärkerschaltung, z.B. mit einem
Operationsverstärker, übertragen. Damit kommen wir zum nächsten Kapitel.
Experiment mit einem Operationsverstärker
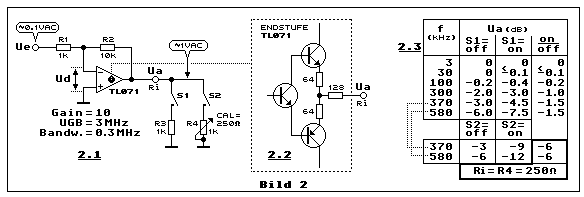
Teilbild 2.1 zeigt eine einfache Verstärkerschaltung mit einem
Operationsverstärker (Opamp) mit einer Verstärkung (Gain) von 10,
definiert mit R1 und R2. R1 ist so gewählt, dass er einen
Sinusgenerator an Ue nur unwesentlich belastet und R2 ist nicht so
gross, dass eine parasitäre Parallelkapazität, sich im oberen
Frequenzbereich signifikant dämfend auswirkt. Als Opamp
dient hier der altbewährte BiFET-Opamp TL071 von
Texas-Instruments mit einem
Verstärkungs-Bandbreite-Produkt von etwa 3 MHz. Für eine Verstärkung
von 10 ergibt dies eine 3-dB-Bandbreite von etwa 300 kHz. Im folgenden
Experiment zeigte sich das verwendete TL071-Exemplar mit einer
Bandbreite von 370 kHz (Streuungseffekt). Man kann das vorliegende
Experiment auch mit andern Verstärkungsfaktoren und ebenso mit andern
Opamps durchführen. Allerdings ändern sich dann auch die Eingangsdaten
und man wird andere Resultate erhalten. Aber man kann den selben Inhalt
erklärend demonstrieren.
Wir wollen indirekt mit ganz einfachen Mitteln untersuchen, wie sich der
Ausgangswiderstand Ri des Opamp in Abhängigkeit der Signalfrequenz an Ue
verhält. Für diesen Test benötigt man nur einen Sinus- oder
Signalgenerator mit Sinusausgang, ein Netzteil mit einer
Ausgangsspannung von ±12 VDC oder ±15 VDC und ein elektronisches
Spannungsmessgerät. Ein unkompliziertes einfaches Oszilloskop wäre
sinnvoll um festzustellen, dass an Ua sicher eine optisch unverzerrte
Sinusspannung anliegt. Von Vorteil wäre es, wenn das Spannungsmessgerät
die Spannungsverhältnisse in Dezibel (dB) angeben kann. Es interessieren
hier nur Spannungsverhältnisse und deshalb werden hier dB-Werte
angegeben. Für die Umrechnung von Dezibel in Spannungsverhältnisse und
umgekehrt gelten die folgenden Formeln mit Beispielen:
Umrechnung von dB zum Zahlenverhältnis:
Ua / Ue = 10 ^ (ndB / 20)
Zahlenbeispiel mit Schaltung in Teilbild 2.1:
10 = 10 ^ (20dB / 20)
Umrechnung des Zahlenverhältnisses in dB:
ndB = 20 * log (Ua / Ue)
Zahlenbeispiel mit Schaltung in Teilbild 2.1:
20dB = 20 * log (10)
Damit die Ausgangsspannung an Ua bei höheren Frequenzen, bedingt durch
die endliche Slew-Rate des Opamp, nicht verzerrt wird, wählen wir eine
niedrige Ausgangsspannung Ua von z.B. 1 VAC (VAC in Effektivwerten). Ue
= 0.1 VAC. Wenn das Messinstrument eine db-Skalierung enthält, kann man
beim Generator auch den Absolutwert von 0 dB einstellen. Dies entspricht
einer Spannung von 0.775 VAC, was per Definition 1 mW an 600 Ohm
entspricht. Trotzdem spielen diese 1 mW und die 600 Ohm hier keine
Rolle. Wer noch nicht weiss, was der Slewrate ist, erfährt man davon
etwas im Elektronik-Minikurs:
Für das Experiment ist die Schaltung von Teilbild 2.1 im Einsatz und wir
tun das was die Tabelle in Teilbild 2.3 illustriert. Wir fahren an Ue
mit der Frequenz von weit unten bei wenigen Hz hoch bis auf 3 kHz. Dabei
schalten wir den Schalter S1 immer wieder ein und aus und beobachten
ganz genau das Messinstrument, welches zwischen Ua und GND angeschlossen
ist. Wir stellen fest, dass die Ausgangs-AC-Spannung Ua konstant bleibt.
Wie erhöhen die Frequenz weiter und erst bei etwa 30 kHz, also bei etwa
1/10 der 3-dB-Grenzfrequenz, stellen wir fest, dass Ua beim Einschalten
von S1 (R3 mit 1 k-Ohm ist eingeschaltet) um weniger als -0.1 dB sinkt.
Der Innenwiderstand Ri des Opamp ist in Relation zum Lastwiderstand R3
also noch immer extrem niederohmig. Dies kommt durch die schnelle
Regelfähigkeit, durch die relativ niedrige Verstärkung von nur 10 und
wegen der sehr hohen offenen Schlaufenverstärkung (Openloop-Gain)
zustande, die allerdings stark abhängig ist von der Frequenz an Ue. Je
höher diese Frequenz ist, um so niedriger ist die Openloop-Gain, und
genau dies beginnt sich oberhalb dieser 30 kHz als wie mehr auszuwirken.
Wir fahren mit der Frequenz weiter hoch bis 100 kHz. Bei offenem
Schalter S1 zeigt sich eine Dämpfung von Ua = -0.2 dB, beim
eingeschalteten S1 sind es -0.4 dB. Man kann auch sagen, dass das
on/off-Verhältnis (siehe Tabelle Teilbild 2.3, vierte Spalte) -0.2 dB
beträgt. Dieses on/off-Verhältnis steigt weiter, je mehr wir die
Frequenz erhöhen. Wir erkennen dies, wenn wir bei zunehmender Frequenz
S1 ständig ein- und ausschalten und am Messinstrument die zunehmenden
Spannungsänderungen beobachten. Bei 100 kHz ist das on/off-Verhältnis
noch -0.2 dB. Bis 370 kHz erhöht sich der Wert kontinuierlich auf -1.5
dB. 370 kHz (anstatt 300 kHz) ist hier die 3-dB-Grenzfrequenz. Erhöhen
wir die Frequenz weiter und zwar gleich auf die mit dem doppelten
Dämpfungswert von -6 dB bei 580 kHz. Wir stellen fest, dass das
on/off-Verhältnis mit einem Wert von -1.5 dB konstant bleibt.
Wir erkennen also zwei Grenzwerte des on/off-Verhältnises. Es ist der
untere Wert von praktisch 0 dB, nämlich bei sehr niedriger Frequenz,
und der obere von -1.5 dB bei hoher Frequenz. Dies gilt für den
Lastwiderstand R3 mit 1 k-Ohm. Wir wollen jetzt mit einem einfachen
Trick herausfinden, wie hoch denn der Innenwiderstand Ri ist, wenn die
Regelgeschwindigkeit des Opamp, bei zu hoher Frequenz, nicht mehr
ausreicht. Diese Situation ergibt sich oberhalb der Grenzfrequenz. Man
beobachte jetzt den unteren Teil der Tabelle im Teilbild 2.3.
S1 bleibt ausgeschaltet. Wenn an Ue die Frequenz 370 kHz (Grenzfrequenz)
beträgt, schalten wir S2 ein und drehen am Potmeter R4 soweit, bis sich
die Spannung an Ua von -3 dB auf -9 dB reduziert hat. Dies ergibt ein
on/off-Verhältnis von -6 dB, entsprechend einem Faktor von 0.5 oder
anders gesagt, Ua ist mit R4 halb so gross wie ohne R4. Nun messen wir
den Widerstand von R4 und damit wissen wir wie gross der praktisch
ungeregelte Innenwiderstand Ri des Opamp ist, weil bei Halbierung der
Spannung Ua mit R4 gilt: Ri = R4.
Bei meinem Experiment zeigte sich ein Wert von etwa 250 Ohm. Bei der
Frequenz von 580 kHz, bei der die Dämpfung von Ua -6 dB beträgt,
bleibt, wie es zu erwarten ist, das on/off-Verhältnis von -6 dB (= 0.5)
gleich gross. Weil R4 Ua ebenfalls um die Hälfte reduziert, gilt, dass
der Innenwiderstand des Opamps identisch ist mit dem Wert von R4. Der
Innenwiderstand des Opamp beträgt also ebenfalls 250 Ohm. Würde man
diesen Opamp nicht als gegengekoppelten Verstärker, sondern als
Komparator einsetzen, reagiert die Ausgangsspannung auf diese
R4-Belastung etwa gleich, weil eben die regelnde Gegenkopplung fehlt.
Bei diesem Versuch darf Ua nicht zu hoch sein, weil sonst ein
Lastwiderstand von nur 250 Ohm den Opamp zu stark belasten und das
Ausgangssignal verzerren (Amplituden klippen) würde. Ua darf für diesen
Versuch problemlos auch kleiner als 1 VAC sein. Anstelle des Potmeter
eignet sich natürlich noch besser eine Widerstands-Dekade, weil man
dann den Widerstand direkt ablesen kann und nicht nachmessen muss.
Die Exemplarstreuungen von Ri können erheblich sein. Werfen wir einen
kurzen Blick in die Endstufe des TL071 (Teilbild 2.2), dann erkennen wir
ausgangsseitig einen Seriewiderstand von 128 Ohm und im Anschluss zu den
Emittern nochmals zusätzlich je 64 Ohm. Einer der 64-Ohm-Widerstände
ist mit der postiven der andere mit der negativen Amplitude an Ua
involviert. Dies ergibt einen Ausgangswiderstand von theoretisch 192
Ohm. Dazu kommt die Streuung dieser Widerstände die unbekannt ist und
ebenfalls unbekannt ist der (statische) Quellwiderstand der Endstufe
ohne diese Widerstände. Der gemessene Wert des Ri von 250 Ohm passt
daher nicht schlecht.
Aber etwas anderes ist für die weitere Betrachtung sehr viel wichtiger,
nämlich die Tatsache, dass sich Ri in Abhängigkeit von der Frequenz,
innerhalb eines gewissen Bereiches, wie eine Induktivität verhält und
das bedeutet nichts anderes, dass eine Verstärkerschaltung immer auch
induktiv ist! Die Bezeichung Ri ist also nicht korrekt, es sollte Zi
heissen, weil wir es mit einem komplexen Ausgangswiderstand, einer
Impedanz, zu tun haben. Wir werden das noch praktisch dadurch erfahren,
dass eine Kapazität am Ausgang einer Verstärkerschaltung, die
Störspannung nicht unbedingt veringert, ja sogar vergrössern oder die
Schaltung sogar zum Oszillieren anregen kann. Man hat einen
unerwünschten Schwingkreis. Dies ist eine wichtige Betrachtung bei
DC-Spannungsreglern, weil man am Ausgang immer Kondensatoren, gerade
wegen der Stabilität, parallel schalten muss. Mit zu niederiger
Kapazität erreicht man allerdings genau das Gegenteil von dem was man
eigentlich will. DC-Spannungsregler sind immer auch
Verstärkerschaltungen.
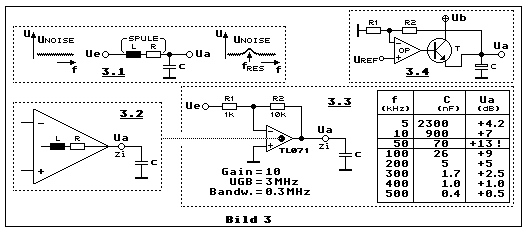
Teilbild 3.1 zeigt uns einen seriellen Resonanzkreis, bestehend
aus einer Induktivität L und einer Kapazität C. Da wir uns mit den
Elektronik-Minikursen stets auf der praktischen Ebene befinden, ist im
Schaltbild gleich der innere ohmsche Verlustwiderstand R, welcher in
Serie zur Induktivität liegt, beigefügt. Es geht dabei um den ohmschen
Widerstand der Spule. Dieser parasitäre Verlustwiderstand R ist in der
Elektronik-Praxis so gut wie immer signifikant. Zwischen den Windungen
und zwischen den Wicklungslagen der Spule gibt es natürlich auch
parasitäre Kapazitäten, die parallel zur Induktivität liegen. Die
Wirkung dieser geringen Kapazitäten kann man hier praktisch
vernachlässigen. Kondensator C ist natürlich keine "stubenreine"
Kapazität. Denken wir uns jedoch mit C einen Papierwickel-, Keramik-
oder sogar einen Alu-Elektrolytkondensator, kann man, je nach Anwendung
oder Betrachtung, den parasitär parallelen und seriellen
(Drahtanschlüsse) ohmschen Widerstand vernachlässigen. Hier trifft das
auf jedenfall zu.
Einen seriellen Resonanzkreis (L und C in Serie) nennt man auch einen
Saugkreis, weil er im Fall der Resonanzfrequenz den maximalen Strom
aufnimmt, - er saugt den Strom quasi an. Die Impedanz erreicht ihren
niedrigsten Wert. Dies hat zur Folge, dass die Spannung über dem
Saugkreis, also zwischen Ue und GND, am geringsten ist, weil die Quelle,
welche Ue speist, praktisch auch nicht beliebig niederohmig ist. Im
Resonanzfall wird die Quelle belastet. Die AC-Spannungen über der Spule
und über dem Kondensator alleine sind aber, wegen des höheren Stromes,
höher als die AC-Spannung an Ue. Zu erklären, warum dies so ist, ist
nicht Gegenstand dieses Elektronik-Minikurses. Dazu gibt es anderweitig
spezielle Grundlagen. Wenn die Verluste, R plus Innenwiderstand der
Spannungsquelle vor Ue, sehr niedrig sind, können diese resonanten
Teilspannungen sehr gross sein. Daher, wenn man an Ue eine weisse
Rauschspannung anlegt, stellt man fest, dass bei der Resonanzfrequenz
fRES die Rauschspannung höher ist und zur
Sinusspannung tendiert. Je weniger Verluste der Resonanzkreis aufweist,
um so mehr tritt die Sinusspannung aus dem niedrigeren Rauschpegel mit
höherer Spannung in den Vordergrund. Dies illustriert das kleine
Diagramm rechts von Ua in Teilbild 3.1. Soviel zur Einleitung für den
weiteren Inhalt...
Teilbild 3.2 drückt symbolisch aus, dass eine Verstärkerschaltung
induktive Eigenschaft hat, wie mit Bild 2 bereits erklärt, allerdings
natürlich nur dann, wenn die Schaltung ein gegengekoppeltes System ist,
wie dies Teilbild 3.3 zum Ausdruck bringt. Wir wollen jetzt untersuchen,
was es mit der Behauptung auf sich hat, dass die Verstärkerschaltung
ein resonantes Verhalten zeigt, wenn parallel zum Ausgang Ua ein
Kondensator C geschaltet ist. Das Experiment mit dem Resultat zeigt die
Tabelle neben der Schaltung:
Bei einer Frequenz von 500 kHz an Ue liegt Resonanz dann vor, wenn die
Kapazität von C 0.4 nF beträgt. Die relative Erhöhung von Ua beträgt
aber nur gerade +0.5 dB. Das kommt daher, dass die ohmschen Verluste
wegen der zu niedrigen inneren Verstärkung (Open-Loop-Gain), bei dieser
hohen Frequenz, relativ gross sind. Man denke an die Tabelle in Teilbild
2.3 und die Erläuterungen dazu.
Je niedriger die Frequenz, um so grösser muss die Kapazität von C sein,
damit Resonanz eintreten kann. Bei 50 kHz haben wir mit C = 70 nF die
grösste relative Erhöhung von Ua = +13 dB. Das ist etwas mehr als ein
Faktor 4! Erhöhen wir die Kapazität weiter und reduzieren die Frequenz,
so dass stets Resonanz eintritt, erkennen wir wie sich die relativen
Spannungserhöhungen reduzieren. Das kommt davon, dass bei niedrigen bis
sehr niedrige Frequenzen, das induktive Verhalten als wie mehr
verschwindet, denn die Impedanz Zi bleibt praktisch gleich sehr
niederohmig. Es ist also eher wieder ein Innen-Widerstand als eine
Innen-Impedanz. Man beachte Tabelle in Teilbild 2.3 bei 3 kHz. Daraus
erkennen wir folgendes: Wenn die Verstärkerschaltung Teil einer
DC-Spannungsregelung (Teilbild 3.4) ist, kann es kontraproduktiv sein,
wenn die Kapazität des Kondensators C am Ausgang, oft ein Elko, zu
niedrig ist. Man merke sich: Die Kapazität des Elko am Ausgang eines
DC-Spannungsreglers muss so gross sein, dass eine möglichst niedrige
Resonanzfrequenz angesprochen wird, damit es diese wegen der fast
fehlenden induktiven Eigenschaft des "inneren Verstärkers" kaum noch
gibt!
Experiment mit einem DC-Spannungsregler
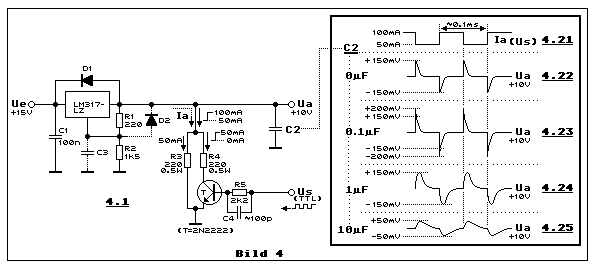
Weil bereits weiter oben ausführlich erklärt, wissen wir, dass wir es
bei einer DC-Spannungsregelung ebenfalls mit induktivem Verhalten,
komplexem frequenzabhängigen Ausgangswiderstand und Problemen bei der
Parallelschaltung mit Kondensatoren am Ausgang zu tun haben. Ich habe
diese Tatsache mit der Lowpower-Version des traditionsreichen
Dreibein-Spannungsreglers LM317, dem LM317LZ geprüft. Nicht mit einer an
Ue überlagerten Rippelspannung mit unterschiedlichen Frequenzen, sondern
mit einer elektronisch geschalteten Last. R3 erzeugt einen Dauerstrom
von Ia = 50 mA. Wenn Transistor T, mit logisch HIGH-Pegel an Us,
eingeschaltet ist, fliesst der doppelte Strom von Ia = 100 mA. Die
Taktfrequenz an Us - es darf ein TTL-Signal sein - beträgt etwa 10 kHz.
Diagramm 4.21 zeigt den mit einem Rechtecksignal geschalteten Strom
zwischen 50 und 100 mA. Diagamm 4.22 zeigt das Einschwingverhalten an
Ua, wenn am Ausgang des DC-Spannungsregler kein Kondensator C2
parallelgeschaltet ist. Die Einschwingspitzenwerte betragen +150 mV und
-150 mV. Wenn man C2 = 0.1 µF zu Ua parallel schaltet, erhöhen sich die
Einschwingspitzenwerte auf +200 mV und -200 mV, wie dies Diagramm 4.23
zeigt. Da meint man es mit dem DC-Spannungsregler gut und möchte, dass
er möglichst schnell die Spannungsspitzen zu niedrigen Werten glättet.
Aber genau bei dieser Überlegung liegt der Denkfehler, weil, wenn es zu
schnell sein soll Resonanzen provoziert werden und darum steigen die
Spannungsspitzen. Diagramm 4.24: Bei C2 = 1 µF hat es
Einschwingspitzenwerte, wie wenn gar kein C2 im Einsatz ist, jedoch mit
wesentlich weniger Anteilen an hohen Frequenzen. Dies erkennt man daran,
dass die Kurvenform nicht mehr so spitz ist. Mit noch weniger Anteilen
an hohen Frequenzen, geht es mit noch höheren Kapazitäten von C2, wie
z.B. mit 10 µF, wie dies Diagramm 4.25 illustriert. Die
Einschwingspitzenwerte sind dabei auf +50 mV und -50 mV reduziert.
Fazit: Die Kapazität von C2 darf problemlos auch wesentlich höher
gewählt werden (z.B. 50 oder 100 µF), damit die Ausgangsspannung noch
besser geglättet ist. Übertreiben muss man aber nicht, denn der
LM317(LZ) ist ein Spannungsregler und kein Referenzspannungs-IC. Dieses
Kapitel soll aber zeigen, dass Daten- und Lehrbücher oft nicht frei sind
von Dogmen und es ist gut, auch diese kritisch zu hinterfragen, so wie
es schliesslich bei weltanschaulichen Inhalten selbstverständlich ist, -
oder jedenfalls sein sollte. Dies passend am Rande vermerkt! ;-)
Der vom Hersteller im Datenblatt empfohlene Kondensator C3 parallel zu
R2, habe ich für dieses Experiment nicht eingesetzt. Man sollte ihn
jedoch für den Einsatz der Schaltung als Spannungsregelung unbedingt
einsetzen und dann darf man auch die Diode D2 nicht vergessen. Anstelle
von bloss 0.1 µF darf C3 ebenso 1 µF, mit natürlich besseren
zusätzlichen Dämpfungswerten der Störspannungen an Ua, aufweisen.
TROBLESHOOTING IN ANALOGSCHALTUNGEN von R. A. Pease
Wenn wir schon beim kritischen Hinterfragen in der elektronischen
Schaltungstechnik angelangt sind, möchte ich auf einen sehr
empfehlenswerten Autor und ein Buch von ihm hinweisen. Es ist R. A.
Pease, der sich auch Bob Pease nennt, und Staff Scientist von
National-Semiconductor in Santa
Clara Kalifornien ist. Sein Buch TROUBLESHOOTING IN
ANALOGSCHALTUNGEN, behandelt u.v.a. das Thema des induktiven
Verhalten von Spannungsreglern. Besonders im Anhang C mit dem Titel
"Störspannungen an Dreibein-Spannungsreglern verstehen und
reduzieren", gibt es sehr interessante Informationen und Diagramme,
die ich hier aus Gründen des Urheberrechts nicht wiedergeben darf. Ich
bin mit meinen Ausführungen zu diesem Thema in diesem
Elektronik-Minikurs einen etwas andern Weg gegangen. Beide Inhalte
ergänzen sich. Ich besitze die deutsche Ausgabe des Buches. Es dürfte
eines der letzten Bücher in deutsch sein, weil Neuaflagen soll es nur
noch in englisch geben. Ich kann dieses Buch von Bob Pease wärmstens
empfehlen!
Es folgt eine einleitende Beschreibung zu diesem Buch. Die Quelle ist
Buch.de. Auf die Wiedergabe der exakten
URL verzichte ich, weil damit zu rechnen ist, dass es diese nicht mehr
lange geben wird. Ich empfehle folgende Suchbegriffe "pease
analogschaltungen" oder "pease troubleshooting" einzugeben. Die
einleitende Beschreibung:
Wer kennt das nicht: Eine Schaltung klemmt, der Grund bleibt
unklar. Mit diesem Buch naht rettende Hilfe. Der Autor erklärt
kompetent und unterhaltsam, wie der verzweifelnde Techniker die Fehler
sucht, ausmacht und beseitigt. Mit ingenieurmässigem, also
pragmatischem Blick - und erfreulich unakademisch - beschreibt er die
Probleme und ihre Lösungen, so dass jeder Schritt zu verstehen und
nachzuvollziehen ist. Ein erfreuliches Buch. Packen wir's an.
Brauchen Sie Hilfe? Bob Pease, ein alter Hase, hilft Ihnen auf seine
direkte Art gern weiter. Bei Philbrick (als der Operationsverstärker
noch in den Kinderschuhen steckte) und National Semiconductor hat er
viele analoge Schaltungen vom Gedanken bis in die Massenproduktion
gebracht und anschliessend auch die Probleme der Anwender bearbeitet.
Jahrzehnte an eigener Erfahrung (und der Fähigkeit, die der anderen zu
nutzen) sowie ein klarer, methodischer Blick, Neugier und das Vermögen,
auch aus Misserfolgen (nicht nur eigener) zu lernen und den Dingen auf
den Grund zu gehen, machen ihn zu einem Mentor, dem man gerne folgt. Die
Grundlage dieses Buches war eine Serie in der Fachzeitschrift EDN in den
USA. Sie überraschte durch ihre Beliebtheit und grosse Leserresonanz. Die
unbefangene Art, Probleme darzustellen, ihre Ursachen zu klären und
damit eine bleibende Behebung anzupacken, hebt sich wohltuend von rein
akademischen Texten ab. Hier hat ein Ingenieur sich mit realen Problemen
auseinander gesetzt und Kopf und Finger benutzt. Das alles beschreibt er
so, dass jeder Schritt zu verstehen und nachzuvollziehen ist. Es gibt
Erfahrungen, die man von anderen lernen kann, ohne sie (meist
unangenehm) selbst zu machen. Besser noch, die Sichtweise, die man dabei
von und mit Bob Pease lernt, hilft mögliche Fallen, Versäumnisse und
Fehlschlüsse zu vermeiden, bevor sie sich auswirken.
Diese Denkweise hilft nicht nur bei analoger Elektronik. Ganz
pragmatisch werden alle Mittel genutzt, die helfen. Würden Sie
glauben, dass ein billiges Taschenradio manchmal besser ist als ein
teurer Messaufbau? Mit kleinen Laboraufbauten, die nur Minuten und
Pfennige kosten, können aufwendige Untersuchungen ausgeschlossen und
der Aufwand in erfolgversprechendere Bahnen gelenkt werden.
Bob Pease hat zu vielen Dingen klare, wohl überlegte Ansichten - und
die spricht er auch deutlich (manchem Posteninhaber wohl zu sehr) und
humorvoll aus. Lassen Sie sich helfen und "die elektronische
Plackerei" zu einer positiven Herausforderung werden, die zum Sieg
über die widerspenstige Materie führt.

Zum Tod von Bob Pease
Zu meiner Schande habe ich erst am Freitag 09.09.2011 durch einen
Kollegen erfahren, dass Bob Pease am 18.06.2011 verstarb. Sein Tod
ist die Folge eines
Autounfalls.
Es folgt gleich im Anschluss zu meinen Worten ein Nachruf vom
Innovationskongress EVERTIQ (http://evertiq.de/news/9911), kopiert als
PDF-Datei, weil man schliesslich nicht sicher sein kann, wie lange eine
News erhalten bleibt und zusätzlich ein Link mit einem Video, der den
berühmten und speziellen Humor von Bob uns stets in guter Erinnerung
halten wird.
In einer Newsletter-Extrabeilage im
ELKO
vom Jahre 2008 schrieb ich, wie ich das grosse Wissen von Bob Pease
persönlich miterleben durfte. Diesen Newsletter möchte ich an dieser
Stelle wiedergeben:
E X T R A - B E I L A G E
=====================================
TROUBLESHOOTING IN ANALOGSCHALTUNGEN
Ursache - Wirkung - Fehlerbeseitigung
-------------------------------------
So lautet der Titel eines Buches von R. A. Pease, das ich
heute empfehlen möchte. Es ist die deutschsprachige Version.
Schon viel länger gibt es das englischsprachige Original.
Ich denke, man übertreibt nicht, wenn man Bob, wie man R. A.
Pease auch nennt, für einen der Analogpaepste hält. Ich
erlebte ihn einmal selbst, als er vor vielleicht einem Jahr
oder auch etwas mehr in Zürich war, und unter der Flagge von
National-Semiconductor ein Analog-Seminar hielt. Mein
Tischnachbar fragte mich vor Beginn wie man ein bestimmtes
schaltungstechnisches Problem lösen könnte. Ich hirnte. Ich
nahm Schreibzeug und Papier und begann mit einem Entwurf. Mein
Tischnachbar und ich bemerkten, dass es schnell recht aufwän-
dig wurde. Ein Opamp reichte nicht. Ich sagte zum Tischnach-
bar, er möge doch in der Pause Pease um Hilfe bitten. Er aber
meinte, er könne ihn doch nicht mit einem solch kniffligen
Problem so lange hinhalten. Ich meinte, er solle es doch
einfach probieren. Die Pause kam, ich ging Kaffe trinken und
der Tischnachbar ging zum "Papst". Als die Pause vorbei war,
fragte ich den Tischnachbarn, wie es klappte. Er legte mir
freudig ein Stück Papier hin und er sagte völlig erstaunt,
dass es kaum eine Minute dauerte und Pease hatte die Lösung
hingekritzelt. Ich verstand zwar sogleich, wie die Schaltung
funktionierte, aber von selbst wäre ich auf die elegante und
einfache Loesung nicht gekommen.
Das Buch, welches ich empfehle, spiegelt den Erfahrungsreich-
tum von R. A. Pease. ISBN: 3-89576-059-5. Es ist ein ELEKTOR-
Buch.
Es folgen jetzt die weiter oben angedeuteten Links:
- National trauert um Analog-Experten Bob Pease
von Anke Schröter (evertiq.de/news/9911) - Remembering Bob Pease: Legendary Analog Expert
Thomas Schaerer, 05.03.2008 ; 12.09.2011 ; 24.11.2014 ; 26.10.2019
