Ganzzahlen / Ganze Zahlen
Ganzzahlen bzw. ganze Zahlen sind Zahlen ohne Nachkommastellen. Die meisten Computersysteme und Programmiersprachen kennen dafür den Datentyp Integer, kurz Int. Je nach Wertebereich auch die Varianten SmallInt und BigInt mit und ohne negativen Vorzeichen (signed bzw. unsigned).
Die Verarbeitung ganzer Zahlen erfolgt in der Informatik in der dualen bzw. binären Darstellung. Dabei entsprechen die Zahlen einer Bitfolge aus Nullen und Einsen.
Nehmen wir beispielhaft einen Wertebereich von 0 bis 15, der sich mit 4 aufeinander folgenden Bits binär darstellen lässt.
0000 = 0 0001 = 1 0010 = 2 0011 = 3 0100 = 4 0101 = 5 0110 = 6 0111 = 7 1000 = 8 1001 = 9 1010 = 10 1011 = 11 1100 = 12 1101 = 13 1110 = 14 1111 = 15
Geht man von einem beispielhaften Datentyp oder einem Datenwort mit 4 Bit Länge aus, dann ermöglicht das 16 Zustände und damit einen Wertebereich für dezimale Ganzzahlen von 0 bis 15. Die "0" steht dabei für "0000" (2) und die "15" für "1111" (2). Das ist der höchste dezimale Nennwert der mit 4 binären Stellen darstellbar ist.
Positionssystem / Stellenwertsystem
Ein Positionssystem, auch Stellenwertsystem genannt, ist ein Zahlensystem, bei dem die Wertigkeit eines Symbols (meist Ziffern oder Zahlen) von seiner Position bzw. seiner Stelle abhängig ist. Der Vorteil von Positionssystemen ist, das mit wenigen Symbolen große Zahlen dargestellt werden können.
Beispiel: Dezimales Zahlensystem
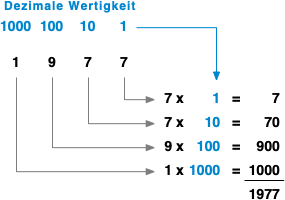
Beispiel: Duales Zahlensystem
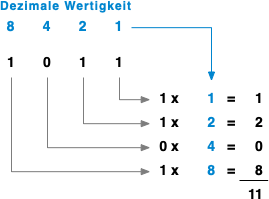
Rechnen mit dualen Zahlen
Die Rechenregeln bei Dualzahlen entsprechen im Prinzip genauso, wie bei Dezimalzahlen. Es gelten jedoch ein paar Besonderheiten bezüglich negativer Zahlen und Zahlen mit Nachkommastellen. Beides gibt es bei dualen Zahlen nicht.
Darstellung negativer Zahlen
Die Darstellung ganzer Zahlen erfordert auch die Darstellung negativer Zahlen. Da das duale Zahlensystem kein negatives Vorzeichen kennt, muss man auf ein Hilfsmittel zurückgreifen. Dabei wird in der Regel das erste Bit einer Bitfolge als Vorzeichenbit missbraucht. Dabei steht die "0" für positive Zahlen und die "1" für negative Zahlen (mit negativem Vorzeichen). Man unterscheidet die Komplement- und die Zweierkomplementdarstellung.
Zur Darstellung und Berechnung positiver wie auch negativer ganzer Zahlen ist die Zweierkomplementdarstellung die gebräuchlichste Form.
Datentypen und Wertebereiche für Ganzzahlen
Je nachdem, wie groß der Wertebereich sein muss, wählt der Programmierer den Datentyp (Variablentyp) für die entsprechende Programmiersprache aus.
Will man mehr als 15 bzw. 7 zählen, dann reichen 4 Bit nicht aus. Zu diesem Zweck gibt es Datentypen, die 1 Byte (8 Bit), 2 Byte (16 Bit), 4 Byte (32 Bit) und 8 Byte (64 Bit) haben. Diese Datentypen existieren dabei ohne Vorzeichen (unsigned) und mit Vorzeichen (signed). Bei letzterem dient das höchstwertige Bit als Vorzeichen. Dabei kommt die Zweierkomplementdarstellung zur Anwendung.
| Wertebereiche mit Vorzeichen (signed) | Speicherbedarf | C#-Datentyp | Delphi | Java-Datentyp | ||
|---|---|---|---|---|---|---|
| -128 ... 127 | - 27 bis 27 -1 | 8 Bit | 1 Byte | sbyte | shortint | byte |
| -32.768 ... 32.767 | - 215 bis 215 -1 | 16 Bit | 2 Byte | short | smallint | short |
| -2.147.483.648 ... 2.147.483.647 | - 231 bis 231 -1 | 32 Bit | 4 Byte | int | integer/longint | int |
| -9.223.372.036.854.775.808 ... 9.223.372.036.854.775.807 | - 263 bis 263 -1 | 64 Bit | 8 Byte | long | int64 | long |
| Wertebereiche ohne Vorzeichen (unsigned) | Speicherbedarf | C#-Datentyp | Delphi-Datentyp | Java-Datentyp | ||
| 0 ... 255 | 0 bis 28 | 8 Bit | 1 Byte | byte | byte | (char) |
| 0 ... 65.535 | 0 bis 216 | 16 Bit | 2 Byte | ushort | word | (char) |
| 0 ... 4.294.967.295 | 0 bis 232 | 32 Bit | 4 Byte | uint | cardinal/longword | (char) |
| 0 ... 18.446.744.073.709.551.615 | 0 bis 264 | 64 Bit | 8 Byte | ulong | (char) | |
Bei der Entscheidung, welcher Ganzzahlen-Datentyp verwendet werden soll, muss der Programmierer abschätzen können, was der kleinste und was der größte Wert ist, der vorkommen kann. Dabei muss er berücksichtigen, dass Zwischenergebnisse während der Berechnung höher oder niedriger liegen können, als das Endergebnis.
Zur Sicherheit einfach mit dem Datentyp zu arbeiten, der den höchsten oder niedrigsten Wert einnehmen kann, ist aber nicht die Lösung. Auf Dauer ist dann unter Umständen mehr als die Hälfte des Speicherplatzes für einen Wertebereich verschwendet, den niemand braucht.
Zahlen in der Informatik
- Zahlen in der Informatik
- BCD-Code - Binary Coded Decimals
- Zweierkomplementdarstellung
- Gleitkommadarstellung / Gleitkommazahlen
- Numerische Datentypen
Weitere verwandte Themen:
Teilen:
Computertechnik-Fibel
Alles was Sie über Computertechnik wissen müssen.
Die Computertechnik-Fibel ist ein Buch über die Grundlagen der Computertechnik, Prozessortechnik, Halbleiterspeicher, Schnittstellen, Datenspeicher, Laufwerke und wichtige Hardware-Komponenten.
Computertechnik-Fibel
Alles was Sie über Computertechnik wissen müssen.
Die Computertechnik-Fibel ist ein Buch über die Grundlagen der Computertechnik, Prozessortechnik, Halbleiterspeicher, Schnittstellen, Datenspeicher, Laufwerke und wichtige Hardware-Komponenten.
Elektronik-Set Raspberry Pi Edition
Elektronik erleben mit dem Raspberry Pi mit Python und GPIO Zero
- Leichter Einstieg ins Hardware-nahe Programmieren mit Python und GPIO Zero
- Experimentieren und Programmieren ohne Vorkenntnisse
- Sofort Loslegen mit All-in-one-Set