Der Transistor-LED- und der FET-Konstantstromzweipol
- Elektronik-Minikurse: Inhaltsverzeichnis WICHTIG: Diverse technische Infos
- Elektronik-Minikurse: Philosophie (Sinn, Vorwissen, Praxisbezug)
- Hilfe bei Leserfragen. (WICHTIG: Unbedingt zur Kenntnis nehmen!)
- Simulieren und Experimentieren, ein Vorwort von Jochen Zilg
- Autor: Thomas Schaerer Opamp-Buch Timer555-Buch
Rückblick auf "Die Transistor-LED-Konstantstromquelle"
Wir blicken zuerst zurück zu Bild 7 des älteren Elektronik-Minikurses mit dem Titel Die Transistor-LED-Konstantstromquelle.... Wir setzen hier fort, wo in diesem früheren Minikurs mit Bild 7 das Thema der Transistor-LED-Konstantstromquelle abgeschlossen wurde. Bild 8 beschliesst diesen früheren Minikurs mit einer Konstantstromquelle, die aus einer Bandgap-Spannungsreferenz und zwei Operationsverstärkern besteht. Wir wollen uns hier jedoch mit einer speziellen Art der Transistor-LED-Konstantstromquelle befassen. Es geht um eine Art kreuzgekoppelter Transistor-LED-Konstantstromquelle, einem Konstantstromzweipol. Doch davon später mehr im Detail. Um diesem Elektronik-Minikurs zu folgen, ist es empfehlenswert den Inhalt des früheren verstanden zu haben. Wir blenden zunächst Bild 7 des früheren Elektronik-Minikurses ein:
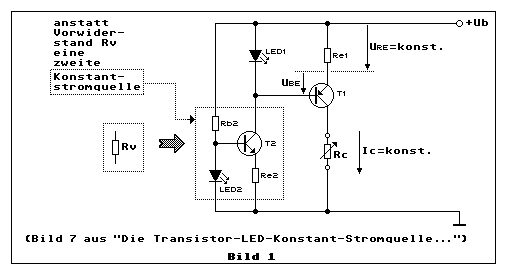
Diese Konstantstromquelle besteht in Wirklichkeit aus zwei
Konstantstromquellen. Die hauptsächliche besteht aus dem PNP-Transistor
T1, aus der LED LED1 als Referenzspannungsquelle und aus dem
Emitterwiderstand Re1. Anstelle von Rv, als Vorwiderstand für LED1,
dient eine weitere zusätzliche Konstantstromquelle. die genau gleich
aufgebaut ist. Einziger Unterschied ist, sie enthält mit T2 einen NPN-
statt einen PNP-Transistor. Was der Zweck dieser zusätzlichen
Konstantstromquelle ist und was die Dimensionierungskriterien sind, ist
im obengenannten
Elektronik-Minikurs
thematisiert.
Würde man LED1 mit einem Vorwiderstand Rv anstelle ebenfalls mit einer
Konstantstromquelle betreiben, wäre die LED1-Referenzspannung und damit
auch der Konstantstrom Ic leicht betriebsspannungsabhängig (+Ub), denn
eine Änderung von +Ub hätte eine Änderung des Stromes in Rv und in der
LED1 zur Folge. Benutzt man anstelle von Rv eine gleichartige jedoch
komplementäre Konstantstromquelle, dann bleibt die Spannung über LED1
von +Ub praktisch unbeeinflusst.
Diese Methode lässt sich zu einer symmetrischen komplementären
Konstantstromquelle erweitern, so dass sich beide Teilstromquellen ihre
Arbeit als Partner teilen und sich gegenseitig in der Unabhängigkeit von
der Betriebsspannung unterstützen. Dieser so genannte
Konstantstromzweipol zeigt im folgenden Kapitel Bild 2.
Die Konstantstromzweipol-Methode
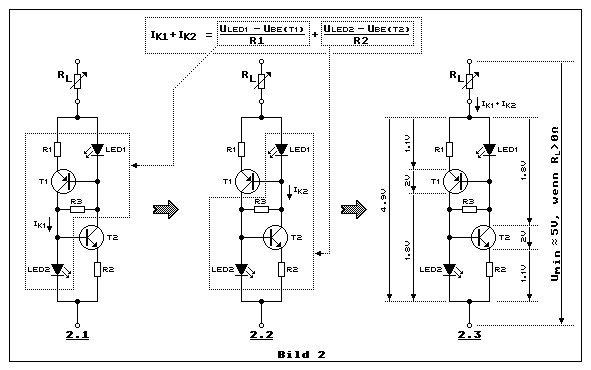
Bild 2 zeigt einen Konstantstromzweipol mit komplementären
Transistoren. Wir betrachten zuerst Teilbild 2.1. Die
Konstantstromquelle mit T1 liefert ihren konstanten Strom Ik1 durch
LED2, welche als Referenzspannung für die Stromquelle mit T2 dient.
Gleichzeitig fliesst Ik1 durch RL. In Teilbild 2.2
liefert die Konstantstromquelle mit T2 ihren konstanten Strom durch
LED1, welche als Referenzspannung für die Stromquelle mit T1 dient.
Gleichzeitig fliesst Ik2 durch RL.
Wir betrachten jetzt exakt die selbe Schaltung noch einmal in Teilbild
2.3. Der konstante Strom durch RL addiert sich aus
Ik1 und Ik2. Diese Konstantstromzweipolschaltung hat gegenüber Bild 1
einen Vor- und zwei Nachteile. Vorteil ist, wir haben eine
Zweipolschaltung. Man kann diese Schaltung direkt in eine dafür
aufgetrennte Leitung einbauen und beide Transistoren beteiligen sich am
Hauptstromfluss. In Bild 1 ist das nicht möglich, denn der nutzbare
Konstantstrom fliesst von Re1 über T1 und Rc nach GND. Nachteilig bei der
Zweipolmethode ist, dass die schwache restliche Temperaturdrift der
beiden Teil-Konstantstromquellen sich addieren und dass die minimale
Spannung über der Stromquelle um eine LED-Spannung höher ist. Für beide
Teile des Konstantstromzweipols gilt die selbe Minimalspannung über der
gesamten Konstantstromschaltung. Diese setzt sich zusammen aus den
beiden LED-Spannungen und aus je einer minimalen
Kollektor-Emitterspannung der beiden Transistoren T1 und T2, damit die
Stromverstärkungsfaktoren vernünftige Werte von etwa 100 oder besser
mehr haben. Es empfiehlt sich daher eine minimale
Kollektor-Emitterspannung von je 2 VDC. Die minimale Spannung Umin
beträgt somit etwa 5 VDC, sofern RL Null Ohm hat.
Die Spannung über RL muss also zu diesen 5
VDC dazu addiert werden. Im Gegensatz zu Bild 1, wo der LED-Strom nur
niedrige Werte von etwa 1 mA haben muss, fliessen durch die LEDs des
Konstantstromzweipols je die Hälfte des Konstantstromes durch
RL. Der LED-Strom kann hier erheblich grösser sein.
Darum ist hier die LED-Spannung einer roten LED mit 1.8 VDC und nicht
mit 1.7 VDC angegeben.
Der aufmerksame Betrachter von Bild 2 fragt sich natürlich, welch
wundersame Aufgabe wohl der Widerstand R3 hat. Er hat die vornehme
Aufgabe des "Zündwiderstandes". Ohne ihn würden sich die beiden
Teilkonstantstromquellen sperren, weil ihre Kollektoresttröme viel zu
niedrig wären. R3 wird sehr hochohmig gewählt. 1 M-Ohm oder besser
grösser. Ein sehr geringe Strom durch ihn reicht um einen
Mitkopplungseffekt in Gang zu setzen, so dass beide Stromquellen
sogleich richtig arbeiten. Man bedenke, das typische Merkmal einer guten
Konstantstromquelle ist ihr hoher Quellwiderstand. Wählt man R3 zu
niederohmig, verschlechtert dies die Konstantstromeigenschaft.
Der geheimnisvolle Widerstand R4
Ein treuer Leser des Elektronik-Kompendium machte mich auf einen Artikel mit dem Thema Konstantstromzweipol in der leider längst ausgestorbenen ELRAD aufmerksam. Man findet ihn in der Januarausgabe des Jahres 1988 auf Seite 47 und er heisst "Grosses Spannungsgebiet". Es geht im Wesentlichen um den selben Artikel wie diesen hier. Allerdings hat der ELRAD-Artikel die Besonderheit des Widerstandes R4, der die Emitter der beiden komplementären Transistoren miteinander verbindet. Diese Besonderheit habe ich hier in leicht gekürzter Form beschrieben. Man beachte Bild 3:
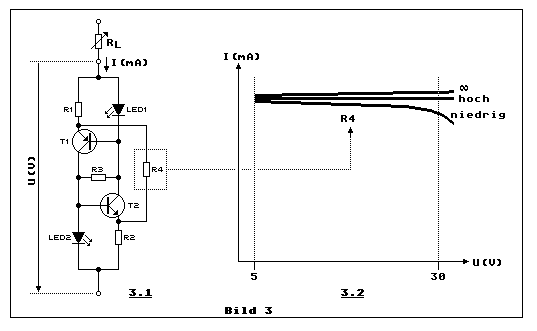
In Teilbild 3.1 ist zusätzlich R4 enthalten. Der Konstantstromzweipol
kommt im Prinzip ohne diesen Widerstand aus und hält auch den Strom über
einen weiten Spannungsbereich konstant. Er hat aber die Eigenschaft,
dass bei zunehmender Spannung über dem Konstantstromzweipol der Strom I
dennoch leicht ansteigt. Mit R4 kann dieser Effekt kompensiert werden.
Wählt man einen zu geringen R4-Wert, wird der Innenwiderstand des
Konstantstromzweipols negativ, so dass bei steigender Spannung der Strom
I sogar abnimmt.
Teilbild 3.2 zeigt das Diagramm mit drei Strom/Spannungs-Kennlinien. Das
Unendlichkeitssymbol bedeutet, dass R4 fehlt. Diese Kennlinie
illustriert wie der Strom bei zunehmender Spannung über dem
Konstantstromzweipol geringfügig ansteigt. Mit hohem R4-Wert lässt sich
die Strom-Spannungskennlinie linearisieren und bei zu niedrigem R4-Wert
wird der Innenwiderstand negativ. Wird der Wert von R4 noch weiter
reduziert, verhält sich der Konstantstromzweipol instabil.
Welchen Wert soll R4 haben? Das ist nicht ganz einfach. Im ELRAD-Artikel
wurde ein fix dimensionierter Konstantstromzweipol vorgestellt und
anstelle der LEDs werden je zwei in Serie geschaltete
Siliziumkleinsignaldioden verwendet. Diese Methode hat einen
signifikanten Nachteil der in
(1)
ausführlich beschrieben ist. Gemäss Dimensionierungsbeispiel im
ELRAD-Artikel mit einem Konstantstrom von etwa 20 mA ergibt sich einen
gerade noch akzeptablen niedrigen R4-Wert von 10 k-Ohm. Der R4-Wert, der
die Strom-Spannungskennlinie linearisiert, kann, je nach Konstantstrom,
einen Wert zwischen einigen k-Ohm bis mehrere M-Ohm haben. Am besten
ermittelt man dies empirisch mit einem Potentiometer oder mit einer
Widerstandsdekade. Man ermittelt den optimalen Wert und baut danach
einen Festwiderstand ein, dessen Wert der Messung am Nächsten kommt.
Vielleicht muss man einen Wert aus der 1%-Widerstandsreihe verwenden.
Durch diesen Abgleich erhöht man den differenziellen Innenwiderstand des
Konstantstromzweipols beträchtlich, was auch richtig ist, denn eine
ideale Konstantstromquelle hat einen unendlich hohen differenziellen
Innenwiderstand.
Der FET-Konstantstromzweipol
Da diese Konstantstromquelle mit einem FET ebenfalls eine
Zweipolschaltung ist, soll sie hier ebenfalls thematisiert werden. Es wird
hier allerdings nur in kurzen Zügen erklärt, weshalb sich ein
selbstleitender Sperrschicht-FET (Junction-FET = JFET) als
Strombegrenzer eignet. Will man tiefer in die Thematik des
Feldeffekttransistors einsteigen, empfehle ich das
Elektronik-Standardwerk Halbleiter-Schaltungstechnik von U.Tietze
und Ch.Schenk. In der neunten Ausgabe gibt es das grosse Kapitel 5 über
Feldeffekttransistoren. Im Unterkapitel 5.5 ist der selbstleitende
JFET als Konstantstromquelle mathematisch ausgiebig beschrieben.
Empfehlenswert ist auch der
JFET-Grundlagenkurs
von Patrick Schnabel.
Ich möchte an dieser Stelle noch auf ein anderes grundlegendes und
praxisnahes Buch mit sehr vielen Anwendungsschaltungen zu den
Feldeffekt-Transistoren hinweisen. Es ist das Buch "FETs und VMOS:
Grundlagen und Anwendung von FETs und Power-MOSFETs" von
Siegfried Wirsum vom Franzis-Verlag (ISBN: 3-7723-6741-0). Ich kaufte
dieses Buch im Jahre 1980. Ob es noch gedruckt und vertrieben wird,
weiss ich nicht. Es macht z.Z. des Schreibens dieses
Elektronik-Minikurses wenig Sinn dies zu evaluieren, denn schliesslich
weiss man nicht, ob es dieses Buch ein Jahr später noch geben wird. Es
bleibt dies also dem Leser überlassen. Ist das Resultat der Suche
negativ, bleiben noch technische Bibliotheken (Hochschulen) und
Antik-Bücherjobs, die es auch im Internet gibt.
Wir betrachten nun den JFET-Konstantstromzweipol in Bild 4:
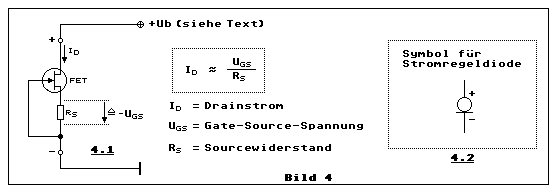
Wir haben es in dieser Schaltung mit einem N-Kanal-JFET zu tun. Der
häufigste N-Kanal-JFET, der in den Elektronik-Minikursen zum Einsatz
kommt, ist der BF245A. Den A-Typ, weil dieser den niedrigsten Drainstrom
(Sättigungsstrom) hat, wenn die Gate-Source-Spannung 0 V beträgt. Der
Drainstrom hat eine Toleranz zwischen 2 und 6.5 mA bei einer
Drain-Souce-Spannung von 15 V. Mehr Infos im
BF245-Datenblatt.
Man beachte Figure 4 "Output characteristics for BF245A; typical
values". Die Diagramme für BF245B (Figure 6) und BF245C (Figure
8) sind nachfolgend auf der selben Seite 5 und auf Seite 6.
Obsolet: Das Problem ist, dass der BF245A,B,C nicht mehr
hergestellt wird. Als Ersatz kann man für den
BF245A
annäherungsweise den
J113
einsetzen. Der
BF256A
würde den BF245A ersetzen. Leider gibt es diesen Typ auch nicht mehr,
jedoch den BF256B, der eigentlich den BF245B ersetzt. Es gibt noch den
PN4393,
jedoch mit einem sehr grossen Toleranzbereich des gesättigten
Drainstromes. Man muss, um den selben niedrigen Drainsättigungsstrom zu
erreichen, den Widerstand Rs ermitteln und einfügen um den selben Wert
zu erreichen wie beim BF245A, wenn bei diesem das Gate direkt mit Source
kontaktiert ist. Dies hat einen Nachteil, der mit Bild 5 im Kapitel
"LED-ON-Anzeige für variable Betriebsspannung" weiter unten
erklärt wird.
Obsolet und doch nicht ganz: Die so eben genannten
BF245(A)-Alternativen (J113 etc.) eignen sich vor allem dann, wenn mit
dem JFET geschaltet wird, wie dies zutrifft in
Synchron-Gleichrichter/JFET-Analog-Schalter I,
Analog-Schalter II und
SC-Tiefpassfilter.
In analogen Anwendungen kann es wünschenwert sein, besonders bei
Reparaturen den originalen BF245 einzusetzen. Die SMD-Version (SOT23)
wird weiterhin von NXP (früher Philips) produziert. Anstelle von BF245
nennt sich dieses Produkt
BF545.
Diesen BF245 (Typen A, B und C) in SMD erhält man bei REICHELT,
RS-ONLINE, CONRAD und FARNELL (Dezember-2017).
Der JFET-Konstantstromzweipol in Bild 4 nutzt die Eigenschaft, dass der
N-Kanal-JFET selbstleitend ist, also bei einer Gate-Source-Spannung von
0 V Strom leitet, bei ansteigender negativer Gate-Source-Spannung den
Drain-Source-Kanal zunehmend abschnürt und oberhalb eines gewissen
Wertes vollständig abschnürt und den Darin-Source-Kanal isoliert.
Selbstverständlich verhält sich der P-Kanal-JFET ebenso, wenn auch mit
umgekehrten Vorzeichen von Strom und Spannung.
Teilbild 4.1: Man schliesse diesen Konstantstromzweipol an eine
variable Spannungsquelle (Netzgerät) und man schützt die Testschaltung
mit einem niedrig eingestellten Begrenzungsstrom von wenigen zehn
Milliampere. Hat man ein solches Netzgerät mit einer einstellbaren
Strombegrenzung nicht zur Verfügung, geht es auch mit einem zur
Ausgangsspannung +Ub in Serie geschaltenen Widerstand, der die
Schutzfunktion übernimmt. Man erhöht langsam die Spannung +Ub, man misst
gleichzeitig den Drainstrom
ID und die Spannung über dem Widerstand Rs.
Dieser entspricht der negativen Gate-Source-Spannung
UGS. Je grösser der Drainstrom, um so grösser die
negative Gate-Source-Spannung. Oberhalb eines bestimmten Wertes der
negativen Gate-Source-Spannung steigt der Drainstrom nicht mehr weiter
an. Auch dann nur noch sehr wenig, wenn man am Netzgerät die
Betriebsspannung wesentlich erhöht. Es hat sich ein Gleichgewicht
zwischen dem Drainstrom und der negativen Gate-Source-Spannung, welche
die Abschnürung des Drain-Source-Kanales bewirkt, eingestellt. Darauf
beruht der Effekt der strombegrenzenden Wirkung dieser einfachen
Schaltung.
Verwendet man für diesen Versuch den JFET BF245A und für den Widerstand
Rs einen Wert von 1 k-Ohm, stellt sich ein stabiler Drainstrom von etwa
1 mA ein. Die Übertragungscharakteristik des BF245A zeigt eine
Gate-Source-Spannung von etwa -1 V bei einem Drainstrom von etwa 1 mA,
wobei die Ausgangscharakteristik in diesem Bereich auch den
Sättigungseffekt in diesem Bereich zeigt, - der Strom ist
spannungsunabhängig relativ konstant. Mit relativ ist zu verstehen, dass
für hochstabile Stromquellen bessere Methoden gibt. Die Berechnung des
Drain-Konstantstromes aus der negativen Gate-Source-Spannung und dem
Widerstand Rs (siehe Formel in Teilbild 4.1) ist nur ein
Annäherungswert, der jedoch für manche Anwendungen ausreicht.
Schliesslich kann man den genauen Stromwert auch empirisch mit einer
Widerstandsdekade ermitteln. Dies dürfte selbst bei präziser Berechnung,
zwecks Nachprüfung, meist notwendig sein.
Wirklich gut funktioniert diese Strombegrenzung nur deshalb, weil der
JFET, wie auch der bipolare Transistor, ein nichtlineares Kennlinienfeld
aufweist. Wenn man beim bipolaren Transistor einen gewissen niedrigen
Basisstrom fliessen lässt, stellt sich, trotz Erhöhen der
Kollektor-Emitter-Spannung oberhalb eines bestimmten Wertes, eine
strombegrenzende Wirkung ein. Beim JFET ist es die
Gate-Source-Vorspannung anstelle des Basisstromes. Oberhalb einer
gewissen Drain-Source-Spannung bleibt der Drainstrom relativ konstant.
Durch die Gegenkopplung mit Rs wird die Stromkonstanz verbessert,
bzw. der differenzielle Innenwiderstand
(dUDS/dID)
der Konstantstromquelle erhöht. Man bezeichnet diesen Innenwiderstand
oft auch als den dynamischen Widerstand. Je nach Betrachtungsweise passt
auch die Bezeichnung Quellwiderstand.
Die Vorspannung zur Strombegrenzung erhält der JFET direkt durch den
Sourcewiderstand Rs. Dies macht diesen Konstantstromzweipol besonders
einfach. Er besteht aus bloss zwei Bauteilen. Es gibt deshalb auch
integrierte JFET-Konstantstromquellen. Weil es Zweipole sind und der
Strom nur in der Richtung von Drain nach Source fliessen darf, nennt man
diese Bausteine auch Feldeffekt-, Konstantstrom- und
Stromregeldioden.
Teilbild 4.2 zeigt das Schaltsymbol für eine solche Stromregeldiode. Es
gibt solche z.B. von den Firmen VISHAY und SILICONIX.
LED-ON-Anzeige für variable Betriebsspannung
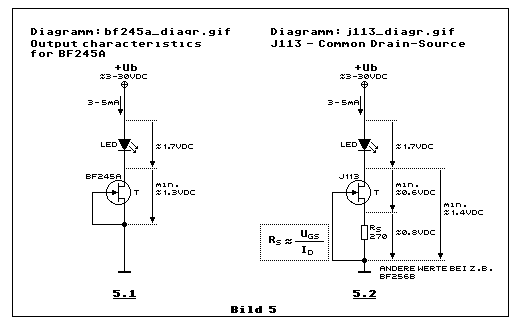
Wenn man eine variable Spannung, z.B. zwischen minimal 3 VDC und maximal
30 VDC mit einer LED anzeigen will, ob die Spannung eingeschaltet ist,
ohne dass diese LED auffällige Schwankungen der Leuchtstärke bei diesem
grossen Spannungsunterschied erzeugt, benötigt man in Serie zur LED,
anstelle eines Widerstandes, eine Konstantstromquelle. Dies geht am
Einfachsten mit einem JFET in der Funktion als Stromregeldiode. Die
etwas schwache Präzision der Stromkonstanz stört bei dieser Anwendung
nicht. Das funktioniert mit einem JFET ohne einen zusätzlichen
Widerstand Rs, wenn der JFET den geeigneten Sättigungsstrom liefert den
man haben will, wie dies Teilbild 5.1 zeigt mit 3 bis 5 mA innerhalb des
so eben genannten Spannungsbereiches.
Mit dem JFET BF245A oder mit einem der erwähnten beinah äquivalenten
Typen geht das problemlos. Bleiben wir zunächst beim BF245A. Als LED
kommt ein rot leuchtender Typ in Frage, weil diese die niedrigste
Flussspannung aufweist. Das ist wichtig, wenn die Anzeige auch bei
möglichst niedriger Spannung von +Ub noch genügend hell leuchten soll.
Diese rot leuchtende LED sollte bei einem Strom von etwa 2 mA, frontal
sichtbar, gut leuchten. Glasklares und nicht mattes Kunstoffgehäuse ist
dabei vorteilhaft.
Die Schwellenspannung einer rot leuchtenden LED liegt bei etwa 1.7 VDC.
Das bedeutet, bei +Ub = 3 VDC, bleibt dem JFET noch eine
Drain-Source-Spannung von etwa 1.3 VDC. Dies ermöglicht gerade noch ein
LED-Strom von knapp 3 mA. Bei +Ub = 5 VDC sind es knapp 4 mA, bei +Ub =
15 VDC etwa 4.5 mA und bei 30 VDC knapp 5 mA. Dies ist ein Beispiel,
gemessen an zwei Exemplaren. Man beachte dazu das
Output-Characteristics-Diagramm des BF245A. Für
diese Anwendung benötigt man keine Berücksichtigung der Streuwerte. Wie
man leicht erkennt, ist die Kurve zwischen einer Drain-Source-Spannung
von etwa 6 VDC bis 15 VDC deutlich idealisiert und dies erst recht bis
zur maximal erlaubten Spannung von 30 VDC (nicht mehr dargestellt). Aber
wie angedeutet, spielt das hier keine Rolle. Die Verlustleistung des
JFET beträgt bei 30 VDC nur etwa 0.15 W.
Logarithmisches Auge: Interessant dabei ist, dass bei einer
Verdopplung des LED-Stromes eine nur sehr geringe Schwankung der
LED-Leuchtstärke wahrnehmbar ist. Dies kommt davon, weil die
Leuchtstärke der LED sich beinahe linear der Stromstärke ändert. Das
Helligkeitsempfinden des menschlichen Auges funktioniert hingegen
logarithmisch. Wenn dem nicht so wäre, wäre es nicht möglich, die Sterne
am klaren Nachthimmel zu sehen und helles Tageslicht zu ertragen. Auch
das Hörempfinden funktioniert logarithmisch.
BF245A-Ersatz: Wenn man an Stelle eines BF245A ein BF256B
einsetzen will, weil man z.B. keinen BF245A mehr besitzt, erhöht sich
bei gleicher Schaltung von Teilbild 5.1 der LED-Strom etwa um den
doppelten Wert. Man kann diesen Strom reduzieren, wenn man mit Hilfe
eines Widerstandes Rs zwischen Source und Gate eine negative
Gate-Source-Spannung erzeugt, wie dies Teilbild 5.2 zeigt. Dies erhöht
um diese Spannung die minimale Spannung +Ub, damit die LED vernünftig
hell leuchten kann. Für den BF256B gibt es im Datenblatt kein
Output-Characteristics-Diagramm. Man muss daher mittels
Potmeter oder Widerstandsdekade den passenden Rs-Wert empirisch
ermitteln.
Im J113-Datenblatt gibt es ein Diagramm mit der Bezeichnung
Common-Drain-Source
Wenn man hier in etwa den selben LED-Strom erzeugen will, muss man, wie
Teilbild 5.2 zeigt, ein Widerstand Rs im Sourcekreis mit einem Wert von
270 Ohm einfügen. Man beachte dazu die Formel zur Berechnung von Rs und
die rot eingezeichnete Information im eben genannten Diagramm. Zwischen
Drain und GND bildet sich die Summe von der Drain-Source-Spannung von
etwa 0.6 VDC und der Gate-Source-Spannung (Spannung über Rs) von etwa
0.8 VDC (Parameter). Dies ergibt eine Spannung von etwa 1.4 VDC bei +Ub
= 3 VDC. Eine etwa ähnliche Situation wie in Teilbild 5.1. Bei
zunehmender Spannung von +Ub steigt auch die Drain-Source-Spannung und
mit ihr nur sehr leicht, wie es sein soll, der LED-Strom
(Drain-Sättigungsstrom).
Wenn man Rs von 270 Ohm in Richtung 100 Ohm reduziert, reduziert sich
die Gate-Source-Spannung von 0.8 VDC in Richtung 0.6 VDC (Parameter) und
der (quasi-)konstante LED-Strom steigt von 3 mA in Richtung 4 mA. Man
ist da fast beliebig frei mit der Wahl des LED-Stromes durch die Wahl
von Rs.
Schaltbox für Netzgeräte
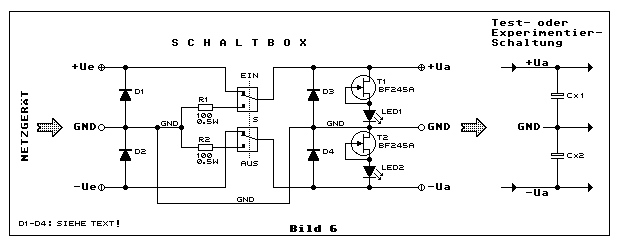
Sinn und Zweck: Eine solche Schaltbox mit einem kleinen Gehäuse
zwischen einem Netzgerät und einer Test- oder Experimentierschaltung
eignet sich hervorragend, wenn man eine solche Schaltung prüfen oder mit
ihr experimentieren will. Der Vorteil einer solchen Schaltbox zeigt sich
vor allem dann, wenn man die Betriebsspannung der Test- oder
Experimentierschaltung oft unterbrechen will. Da ist es sinnvoll, dass
man nicht ständig das Netzgerät ein- und ausschalten muss, weil der
Netzschalter schliesslich eine begrenzte Lebensdauer hat und man nach
dem Ausschalten darauf achten muss, dass die Spannung auch wirklich auf
dem GND-Pegel liegt, bevor man aktiv wird. Selbstverständlich hat auch
der Kippschalter S in der Schaltbox eine begrenzte Lebensdauer. Es ist
aber deutlich weniger umständlich diesen Schalter auszutauschen, als den
des Netzgerätes, den man, weil speziell, oft extra bestellen muss. Dazu
kommt noch, dass man für das Ein- und Ausschalten des Netzgerätes lästig
den Arm strecken muss, um den Schalter zu erreichen, weil das Netzgerät
oft nicht gerade zuvorderst auf dem Labortisch platziert ist. Das wäre
ein weiteres Argument für eine kleine Schaltbox in der Nähe des
Geschehens. Ich habe mir längst drei solche Boxen gebaut, die mir den
Elektronik-Alltag oft erleichtern.
Die Schaltung der Schaltbox in Bild 6: Eigentlich genügt für S
ein zweipoliger EIN/AUS-Schalter, um ±Ua für die folgende Schaltung ein-
und auszuschalten. Hier gleich angemerkt, man kann auch nur, je nach Art
der Test- oder Experimentierschaltung, +Ue-->+Ua oder -Ue--->-Ua
(Single-Supply-Mode) verwenden. Der zweipolige Umschalter S dient dem
Zweck, dass beim Ausschalten ±Ua sofort auf den GND-Pegel schaltet. Das
ist dann wichtig, wenn in der Test- oder Experimentierschaltung
Block-Kondensatoren Cx1 und/oder Cx2 im Einsatz sind. Sind es nur
keramische Kondensatoren (Kerkos) im Bereich von 100 nF in der Nähe an
der Speisung von digitalen und analogen ICs, kann man dann auf die
Entladung mittels Umschalter verzichten, wenn die Anzahl dieser Kerkos
so gering ist, dass beim Ausschalten genügend Entladestrom durch die
Schaltung selbst fliesst, so dass an ±Ua den GND-Pegel rasch erreicht
wird.
Gehen wir davon aus, dass dies nicht immer der Fall ist und bei einer
Test- oder Experimentierschaltung die Cx1- und/oder Cx2-Werte im 100-
oder 1000-µF-Bereich haben, dann muss mittels zweipoligem Umschalter im
Aus-Zustand ein kurzzeitiger Entladestrom von Cx1 (+Ua) über R1 nach GND
fliessen. Dasselbe gilt bei Bedarf von Cx2 (-Ua) über R2 nach GND.
Nehmen wir mal an Cx1 ist ein Elko mit einer Kapazität von 1000 µF. Beim
Entladen über R1 mit 100 Ohm wirkt eine Zeitkonstante von 0.1 s. Bei der
5-fachen Zeitkonstante, also nach einer halben Sekunde, hat sich +Ua
soweit reduziert, dass es fast dem GND-Pegel entspricht. Wartet man eine
volle Sekunde, kann man problemlos ohne Risiko in der Test- oder
Experimentierschaltung herum hantieren. Die maximale Betriebsspannung
ist vorgegeben durch die JFETs mit einer maximal zulässigen
Drain-Source-Spannung von 30 V.
Angenommen Cx1 = Cx2 = 1000 µF. Wie gross muss die Leistung von R1 und
R2 sein? Wenn konstant 30 VDC an R1 oder/und R2 mit je 100 Ohm anliegen,
sind das je 9 W. Diesen Zustand gibt es jedoch nicht.Allerdings genügt
ein 0.5W-Widerstand, weil die Wärmeträgheit eines solchen Widerstandes
gross genug ist, dass sogar bei einem 0.25W-Widerstand keine spürbare
Erwärmung entsteht beim Ausschaltvorgang, wenn die Wartezeit bis zum
nächsten Ausschalten gross genug ist.
Dies kann man leicht einhalten. Wenn man auch nur gerade während einer
Minute ein Test mit der angeschlossenen Schaltung durchführt, wird bis
zum nächsten Ausschalten, und man wiederholt diesen Vorgang, ein
Tastgrad von etwa 1/600 erzeugt, was an R1 und/oder R2 eine
durchschnittliche Leistung von 15 mW erzeugt. Ein einfacher Praxistest
mit einem 0.25W-Widerstand mit 100 Ohm und einem wilden Ein- und
Ausschalten mit dem Umschalter S, wodurch der Tastgrad kleiner wird,
reicht aus, dass der 1/4W-Widerstand zwar so heiss wird, dass man ihn
gerade nicht mehr berühren will. Das zeigt, R1 oder R2 sind weit davon
entfernt bei dieser wilden Schalterei beschädigt zu werden. Mit je einem
1/2W-Widerstand ist man auf der ganz sicheren Seite, dass nichts
passieren kann. Die Kapazität von Cx1 und Cx2 dürfen dann auch deutlich
grösser sein.
Wieso gerade 100 Ohm für Rs und nicht weniger? Wenn S ausgeschaltet ist
und man will mit einem Durchgangsprüfer die Test- oder
Experimentierschaltung testen, piepst der Durchgangsprüfer von guter
Qualität bei 100 Ohm nicht. Oder er piepst, aber er zeigt am Display die
Spannung über dem Widerstand an. 10 Ohm für Rs können dabei etwas knapp
sein. Mit diesem
Selbstbau-Verdrahtungstester
(Schaltung) kann man
die Ansprechschwelle des Piepstones locker auf 1 Ohm einstellen.
Die Dioden D1 bis D4 dienen dem Verpolungsschutz. Grundsätzlich genügen
D1 und D2. D3 und D4 dienen zusätzlich dem Zweck, wenn man bei offenem
Schalter S die Test- oder Experimentierschaltung mit geladenen Cx1 und
Cx2 falsch gepolt an die Ausgangsbuchsen der Schaltbox anschliesst. D3
und D4 entladen Cx1 und Cx2 sofort.
Vor allem D1 und D2 müssen dem maximalen Strom des Netzgerätes angepasst
sein. Dies bedeutet, dass das Netzgerät eine einstellbare Strombegrezung
haben muss. Ist dies nicht der Fall sollte man flinke Schmelzsicherungen
in Serie zu +Ue und -Ue schalten. Für einen Maximalstrom von 3 A an +Ue
und -Ue, empfiehlt es den bekannten Leistungsdioden
1N5402
einzusetzen.
Thomas Schaerer, 17.06.2001, 01.07.2001 ; 02.12.2002 ; 14.03.2003(dasELKO) ; 04.12.2004 ; 14.06.2006 ; 23.06.2011; 15.12.2017
