Raspberry Pi Pico: Einfaches neuronales Netz trainieren und anwenden (KI)
Die ursprüngliche Zielsetzung war, ein ganz einfaches neuronales Netz auf dem Raspberry Pi Pico mit MicroPython zu trainieren und anzuwenden. Was sich im ersten Moment in dieser Kombination auszuschließen scheint, ist durchaus möglich. Es geht dabei weniger um eine ersthafte Anwendung, sondern eher um eine Demonstration, um einen Eindruck zu bekommen, wie ein neuronales Netz funktioniert.
Neuronale Netze sind ein spezieller Ansatz im maschinellen Lernen, inspiriert vom menschlichen Gehirn.
Es handelt sich um ein Minimalbeispiel für das Training und die Anwendung eines neuronalen Netzes. Das eigentliche Lernobjekt für das neuronale Netz ist die Funktionsweise der logischen Funktion XOR. Das ist die kleinste Funktion, die ein neuronales Netz nicht-linear modellieren muss.
Natürlich ist die Wahrheitstabelle eines XOR bekannt und muss deshalb eigentlich nicht gelernt werden.
Ein neuronales Netz die Funktionsweise eines XOR lernen zu lassen hat mehrere Vorteile:
- Weil das XOR bekannt ist, kann man leicht prüfen, ob das Modell richtig gelernt hat.
- Die notwendigen Trainingsdatensätze lassen sich leicht erzeugen.
- Die Anforderungen an Rechenleistung und Speicher sind minimal und das Training ist schon nach wenigen Sekunden abgeschlossen.
- Das Modell lässt Spielraum, um mit seinen KI-spezifischen Parametern zu experimentieren, um die Funktionsweise besser zu verstehen.
Das folgende Beispiel demonstriert die Machbarkeit von Training und Anwendung von KI-Modellen auf eingeschränkter Hardware. Hier ist es ein Raspberry Pi Pico mit MicroPython.
Das Besondere dabei:
- Der Programmcode beinhaltet die typischen Funktionen, die neuronale Netze haben.
- Du kannst dem Training live zuschauen. Du kannst beobachten, wie das neuronale Netz besser wird.
- Der Programmcode ist so minimal, dass du die verschiedenen Funktionen und Prozesse innerhalb eines KI-Trainings nachvollziehen kannst.
- Das Beispiel erlaubt dir andere logische Funktionen lernen zu lassen. Zum Beispiel AND oder OR.
Übersicht: Grundlagen zur künstlichen Intelligenz (KI)
- Künstliche Intelligenz (KI) / Artificial Intelligence (AI)
- Machine Learning / Maschinelles Lernen
- Künstliche neuronale Netze (KNN)
Warum ausgerechnet das XOR lernen?
In den 1960ern zeigten Marvin Minsky und Seymour Papert, dass ein einlagiges Perzeptron (ein einfaches neuronales Netzwerk mit einer Schicht) nicht in der Lage ist, die Funktionsweise eines XOR zu lernen, weil es nur linear trennbare Probleme lösen konnte. Das führte damals zu viel Skepsis gegenüber künstlichen neuronalen Netzwerken.
Es motivierte die Entwicklung von mehrschichtigen Netzwerken (Multilayer Perceptrons), die mit einer nichtlinearen Aktivierungsfunktion (z. B. Sigmoid, ReLU) das XOR-Problem lösen konnten.
Um XOR zu lernen, braucht ein neuronales Netz:
- Mindestens eine versteckte Schicht (hidden)
- Nichtlineare Aktivierungsfunktionen (z. B. Sigmoid)
Das war der Beweis, dass man mit mehr Schichten (heute nennt man das „tiefes Lernen“) auch nichtlineare Entscheidungsgrenzen lernen kann.
Das XOR-Problem ist also ein Lehrbeispiel, das zeigt, dass neuronale Netzwerke mit mehreren Schichten und nichtlinearer Aktivierung notwendig sind, um komplexe, nichtlinear trennbare Funktionen wie XOR zu lernen.
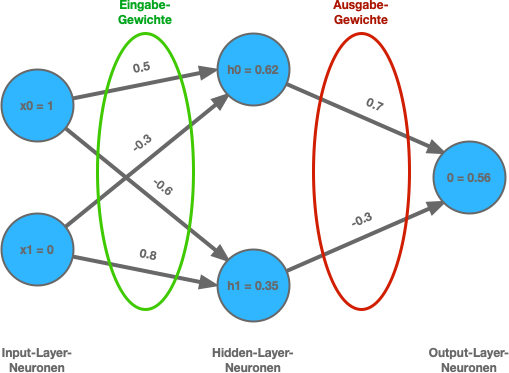
Das hier verwendete neuronale Netzwerk hat:
- 2 Eingänge
- 1 versteckte Schicht mit 2 Neuronen
- 1 Ausgang
Programmcode
Die Implementierung eines künstlichen neuronalen Netzes im folgenden Programmcode berücksichtigt Feedforward, Backpropagation und Training über viele Epochen. Wenn du diese KI-spezifische Fachbegriffe, speziell für neuronale Netze, noch nicht kennst, dann empfiehlt es sich, dass du dich ein wenig vorab informierst.
Hinweis: Es ist nicht notwendig, den Programmcode in seiner Gesamtheit zu verstehen und nachzuvollziehen.
# Biblotheken laden
#import time
# Sigmoid-Funktion und Ableitung
def sigmoid(x): return 1 / (1 + pow(2.71828, -x))
def sigmoid_derivative(x): return x * (1 - x)
# Trainingsdatensätze (4)
# Eingänge [A, B] einer logischen Funktion
inputs = [ [0, 0], [0, 1], [1, 0], [1, 1] ] # nicht ändern
# Ausgang der logischen Funktion
targets = [ [0], [1], [1], [0] ] # XOR
#targets = [ [0], [0], [0], [1] ] # AND
#targets = [ [0], [1], [1], [1] ] # OR
#targets = [ [1], [1], [1], [0] ] # NAND
# Startgewichte mit festgelegten Werten
w_input_hidden = [[0.5, -0.6], [-0.3, 0.8]] # 2x2
w_hidden_output = [0.7, -0.5] # 1x2
# Startgewichte mit zufälligen Werten
#import random
#w_input_hidden = [[random.uniform(-1, 1), random.uniform(-1, 1)], [random.uniform(-1, 1), random.uniform(-1, 1)]]
#w_hidden_output = [random.uniform(-1, 1), random.uniform(-1, 1)]
# Biases (nicht ändern)
b_hidden = [0.0, 0.0]
b_output = 0.0
# Lernrate
lr = 0.5 # lernt gut (Standardwert)
#lr = 0 # lernt nichts
#lr = 100 # Netz instabil (explodiert)
#lr = 10 # instabil / osziliert
#lr = 1 # lernt schneller
#lr = 0.1 # lernt langsamer
# Anzahl der Durchläufe (Epoche)
EPOCHS = 2000
print()
print('Training eines neuronalen Netzes')
print()
print(' Epochen:', EPOCHS)
print('Lernrate:', lr)
for epoch in range(EPOCHS+1):
if epoch % 100 == 0:
print()
print('Epoche', epoch)
print()
# Start der Epoche mit Fehler = 0
total_error = 0
# Eingangszustände
for i in range(4):
x = inputs[i]
y = targets[i][0]
#if epoch % 100 == 0: print(f"Beispiel {i+1}: Eingabe: {x}, Ziel: {y}")
# Forward Pass: Eingabe -> Hidden
h_input = [0, 0]
h_output = [0, 0]
# Diese Schleife verarbeitet jedes Neuron im Hidden Layer
for j in range(2):
# Berechnet für jedes Neuron den gewichteten Eingang
h_input[j] = x[0] * w_input_hidden[0][j] + x[1] * w_input_hidden[1][j] + b_hidden[j]
# Berechnet für jedes Neuron die Aktivierung durch die Sigmoid-Funktion
h_output[j] = sigmoid(h_input[j]) # Ausgabe des Hidden-Neurons
#if epoch % 100 == 0: print(f" Hidden-Layer-Aktivierungen: {['%.3f' % h for h in h_output]}")
# Forward Pass: Hidden -> Output
# Ausgabe der Hidden-Neuronen wird gewichtet aufs Ausgabeneuron summiert
o_input = h_output[0] * w_hidden_output[0] + h_output[1] * w_hidden_output[1] + b_output
# Sigmoid-Aktivierung für den finalen Output
o_output = sigmoid(o_input)
#if epoch % 100 == 0: print(f" Netzwerk-Ausgabe: {o_output:.3f}")
# Fehler der Vorhersage wird berechnet (Differenz zur Zielausgabe)
error = y - o_output
# Der quadratische Fehler fließt in die Statistik ein
total_error += error ** 2
#if epoch % 100 == 0: print(f" Fehler: {error:.3f}")
# Backpropagation: Output-Layer
# Delta für den Output-Layer wird berechnet
d_output = error * sigmoid_derivative(o_output) # unter Berücksichtigung der Ableitung der Sigmoid-Funktion
# Gewichte Hidden: Output anpassen
# Aktualisiert die Gewichte vom Hidden-Layer zum Output-Layer
for j in range(2):
delta_w = lr * d_output * h_output[j]
#if epoch % 100 == 0: print(f" w_hidden_output[{j}]: {delta_w:.4f}")
w_hidden_output[j] += delta_w
# Bias des Output-Neurons wird angepasst
b_output += lr * d_output
#if epoch % 100 == 0: print(f" bias_output: {lr * d_output:.4f}")
# Backpropagation: Hidden Layer (Fehler und Updates)
for j in range(2):
# Fehlersignal (Delta) für das Hidden-Neuron j
d_hidden = d_output * w_hidden_output[j] * sigmoid_derivative(h_output[j])
# Gewichtsänderungen in Abhängigkeit von Lernrate (rt), Fehlersignal (d_hidden) und der Signale an den Eingängen (x)
delta_w0 = lr * d_hidden * x[0]
delta_w1 = lr * d_hidden * x[1]
#if epoch % 100 == 0: print(f" w_input_hidden[0][{j}]: {delta_w0:.4f}, w_input_hidden[1][{j}]: {delta_w1:.4f}")
# Gewichtsänderungen zu den aktuellen Gewichten addieren
w_input_hidden[0][j] += delta_w0
w_input_hidden[1][j] += delta_w1
# Bias des Hidden-Neurons j wird angepasst
b_hidden[j] += lr * d_hidden
#if epoch % 100 == 0: print(f" bias_hidden[{j}]: {lr * d_hidden:.4f}")
if epoch % 100 == 0:
print(f" Gesamtfehler: {total_error:.4f}")
#time.sleep(1)
# Nach dem Training: Testausgabe
print()
print('Test nach Training (Inferencing)')
print()
for x in inputs:
h_output = [0, 0]
for j in range(2):
h_output[j] = sigmoid(x[0] * w_input_hidden[0][j] + x[1] * w_input_hidden[1][j] + b_hidden[j])
o_output = sigmoid(h_output[0] * w_hidden_output[0] + h_output[1] * w_hidden_output[1] + b_output)
print(f"Eingabe: {x} -> Ausgabe: {o_output:.3f} -> {'1' if o_output > 0.5 else '0'} (erwartet: {targets[inputs.index(x)]})")
# Model in Datei speichern
filename = 'xor_model.txt'
with open(filename, 'w') as file:
# Schreibe Gewichte und Biases zeilenweise
for row in w_input_hidden:
file.write(",".join(str(w) for w in row) + "\n")
file.write(",".join(str(w) for w in w_hidden_output) + "\n")
file.write(",".join(str(b) for b in b_hidden) + "\n")
file.write(str(b_output) + "\n")
print()
print('Neuronales Netz in der Datei', filename, 'gespeichert.')
Beobachtungen (Erläuterungen zur Datenausgabe)
Die Textausgabe auf der Kommandozeile ist so gestaltet, dass man dem neuronalen Netz beim Lernen zusehen kann. Das Training läuft relativ schnell ab, sodass man eventuell die Geschwindigkeit künstlich reduzieren muss (mit time.sleep).
Mit print()-Ausgaben lässt sich der Lernprozess Schritt für Schritt beobachten. Standardmäßig wird nur der Gesamtfehler innerhalb einer Epoche (ein Durchlauf der gesamten Trainingsdaten) angezeigt. Alle anderen berechneten Werte sind auskommentiert und können nach Bedarf angezeigt werden. Zu beobachten ist, dass der Gesamtfehler im Verlauf des Trainings reduziert wird.
Ein anfänglicher Fehleranstieg beim Training ist normal. Er entsteht durch ungünstige Gewichtswahl, Lernraten oder komplexe Fehlerlandschaften. Entscheidend ist, dass der Fehler im Verlauf des Trainings insgesamt sinkt.
Nach dem Training werden alle XOR-Eingangs-Kombinationen getestet. Das Test-Ergebnis wird vermutlich ein richtiges Ergebnis liefern. Das sieht man daran, dass die Ausgabe dem erwarteten Ergebnis für jede Eingabe-Kombination entspricht.
Experimente
Du hast den Programmcode zum Trainieren eines neuronalen Netzes ausprobiert und fragst Dich, was du damit jetzt machen kannst:
- Anzahl der Epochen erhöhen
- Startgewichte ändern
- Lernrate verändern
- Andere logische Funktion lernen
- KI-Modell anwenden (Inferencing)
Hinweis: Ob das Training gut oder weniger gut funktioniert, kannst du am Gesamtfehler ablesen. Der Gesamtfehler muss pro Epoche immer geringer werden. Optimalerweise muss er bei diesem KI-Modell unter „0.01“ liegen, damit es korrekt funktioniert.
1. Experiment: Anzahl der Epochen verringern
Die Anzahl der Epochen gibt an, wie oft das gesamte Trainingsset dem neuronalen Netz gezeigt wird. Sie hat einen direkten Einfluss auf den Lernfortschritt. Aber mehr Epochen sind nicht automatisch besser. In der Praxis kann ein KI-Model überlernen (Overfitting). In diesem Modell ist das nicht der Fall. Mit einer höheren Anzahl von Epochen sinkt die Fehlerrate und es erhöht sich die Wahrscheinlichkeit für ein richtiges Ergebnis. Du kannst die Anzahl der Epochen auch einfach mal verringern, um festzustellen, bei wie vielen Durchläufen das Ergebnis nicht mehr korrekt ist.
2. Experiment: Startgewichte ändern
Die Startgewichte haben einen entscheidenden Einfluss darauf, wie (und ob) ein neuronales Netz lernt. Sie sind der Startpunkt des Lernprozesses. Je nachdem, wie sie gewählt werden, kann das Netz gut lernen, sehr langsam lernen oder im schlechtesten Fall gar nicht lernen.
Beim Training wird das Netz von den initialen Gewichten aus Stück für Stück angepasst. Sind die Startwerte ungünstige gewählt, dann kann es lange dauern, bis das Netz überhaupt erkennt, in welche Richtung es sich verbessern soll. Dadurch lernt es nur sehr langsam oder vielleicht sogar gar nicht.
Die Gewichte dürfen nicht „0.0“ sein. Sie dürfen auch nicht zu groß (10) oder symmetrisch (0.5, 0.5) sein. Bei letzterem würden die Hidden-Neuronen dasselbe Signal bekommen und sich identisch verhalten.
Funktionierende Werte liegen zwischen „-1.0“ und „1.0“. Aber nicht kleiner als „-0.1“ oder „0.1“. Wenn man möchte, dann kann man auch mit jeweils zufälligen Werten starten.
3. Experiment: Lernrate ändern
Die Lernrate nimmt Einfluss auf die Gewichtsveränderung. Dabei ist eine zu große Lernrate gar nicht gut, weil das dazu führen kann, dass die Fehlerrate gleich bleibt oder immer mal wieder steigt und durch mehr Epochen erneut verringert werden muss.
4. Experiment: Andere logische Funktion lernen
Es gibt noch weitere logische Funktionen. Indem Du andere „targets“ wählst, das sind die zu lernenden Ausgangszustände, kannst du eine andere logische Funktionen lernen (trainieren) lassen.
Interessant ist das deshalb, weil es logische Funktionen gibt, die weniger Epochen zum Lernen brauchen, sich also schneller lernen lassen.
5. Experiment: KI-Modell anwenden (Inferencing)
In der Datei „xor_model.txt" werden die gelernten Gewichte und Biases des Modells gespeichert. Diese Datei ermöglicht es, die gelernten Gewichte und Biases später in einem Programm zu laden, um das Modell für Inferencing zu nutzen.
# Sigmoid-Funktion und Ableitung
def sigmoid(x): return 1 / (1 + pow(2.71828, -x))
# Alle möglichen Eingabekombinationen
# Eingänge [A, B] einer logischen Funktion
inputs = [[0,0],[0,1],[1,0],[1,1]]
# Modell laden
print('Neuronales Netz laden')
print()
filename = 'xor_model.txt'
with open(filename) as file:
lines = file.read().splitlines()
w_input_hidden = [list(map(float, lines[0].split(","))), list(map(float, lines[1].split(",")))]
w_hidden_output = list(map(float, lines[2].split(",")))
b_hidden = list(map(float, lines[3].split(",")))
b_output = float(lines[4])
# Hauptlogik
print('Inferenz mit geladenem Modell')
print()
# Diese Schleife durchläuft alle Eingabekombinationen
for x in inputs:
# Initialisiert die Ausgabe des Hidden Layers mit zwei Neuronen.
h_output = [0, 0]
# Diese Schleife berechnet die Aktivierung jedes Neurons im Hidden Layer.
for j in range(2):
# Berücksichtigt die Gewichte, Bias und Aktivierung
h_output[j] = sigmoid(x[0] * w_input_hidden[0][j] + x[1] * w_input_hidden[1][j] + b_hidden[j])
# Berechnet die Ausgabe des Netzes
o_output = sigmoid(h_output[0] * w_hidden_output[0] + h_output[1] * w_hidden_output[1] + b_output)
# Gibt die Eingabe und die ermittelte Ausgabe aus
print(f"Eingabe: {x} -> Ausgabe: {o_output:.3f} -> {'1' if o_output > 0.5 else '0'}")
Raspberry Pi Pico: Neuronales Netz mit Daten von einem MPU-6050 trainieren
In diesem KI-Projekt wird ein einfacher Ansatz zur Bewegungserkennung mithilfe eines neuronalen Netzes direkt auf einem Raspberry Pi Pico umgesetzt. Ein MPU-6050-Sensor erfasst Beschleunigungs- und Rotationsdaten, aus denen charakteristische Muster für bestimmte Bewegungen wie z. B. „ruhig“ oder „schütteln“ extrahiert werden.
Das Projekt zeigt, dass auch auf einem Mikrocontroller mit begrenzten Ressourcen einfache KI-Anwendungen ohne externe Tools, Lösungen und Dienste realisierbar sind. Alle Programmcodes laufen auf einem Raspberry Pi Pico.
Weitere verwandte Themen:
- Raspberry Pi Pico: Künstliche Intelligenz (KI)
- Raspberry Pi Pico: Smart Home (Ideen und Projekte)
- Raspberry Pi Pico: Internet of Things (IoT)
- Raspberry Pi Pico: 10 nützliche Anwendungen und Projekte zum Nachbauen
- Raspberry Pi Pico: 10 einfache Experimente
Frag Elektronik-Kompendium.de
Hardware-nahes Programmieren mit dem Raspberry Pi Pico und MicroPython
Das Elektronik-Set Pico Edition ist ein Bauteile-Sortiment mit Anleitung zum Experimentieren und Programmieren mit MicroPython.
- LED: Einschalten, ausschalten, blinken und Helligkeit steuern
- Taster: Entprellen und Zustände anzeigen
- LED mit Taster einschalten und ausschalten
- Ampel- und Lauflicht-Steuerung
- Elektronischer Würfel
- Eigene Steuerungen programmieren
Online-Workshop: Programmieren mit dem Raspberry Pi Pico
Gemeinsam mit anderen und unter Anleitung experimentieren? Wir bieten unterschiedliche Online-Workshops zum Raspberry Pi Pico und MicroPython an. Einführung in die Programmierung, Sensoren programmieren und kalibrieren, sowie Internet of Things und Smart Home über WLAN und MQTT.
Besuchen Sie unser fast monatlich stattfindendes Online-Meeting PicoTalk und lernen Sie uns kennen. Die Teilnahme ist kostenfrei.






