Verstärkung und Dämpfung
In der Signaltechnik werden Leistungen und Spannungen über das logarithmische Verhältnis ausgerechnet und in Verstärkung/Dämpfung oder Pegel angegeben.

- Verstärkung liegt dann vor, wenn das Ausgangssignal größer als das Eingangsignal ist.
- Dämpfung liegt dann vor, wenn das Ausgangssignal kleiner als das Eingangssignal ist.
Obwohl man Verstärkung und Dämpfung separat voneinander berechnen kann, berechnet man in der Praxis nur die Verstärkung. Hierbei wird das Ausgangssignal mit dem Eingangssignal dividiert. Ist das Ergebnis positiv handelt es sich um eine Verstärkung. Ist das Ergebnis negativ handelt es sich um eine Dämpfung. Das vereinfacht weitere Berechnungen und man sieht auf den ersten Blick, ob man es mit Verstärkung oder Dämpfung zu tun hat. Positives Ergebnis bedeutet Verstärkung und negatives Ergebnis bedeutet Dämpfung.
Formeln für die Verstärkung
- A (dB) = 20 * log (Ua / Ue)
- A (dB) = 20 * log (Ia / Ie)
- A (dB) = 10 * log (Pa / Pe)
Rechnet man mit einer Verstärkungsformel und das Ergebnis ist negativ, dann hat man eine Dämpfung.
Formeln für die Dämpfung (Attenuation)
- a (dB) = 20 * log (Ue / Ua)
- a (dB) = 20 * log (Ie / Ia)
- a (dB) = 10 * log (Pe / Pa)
Rechnet man mit einer Dämpfungsformel und das Ergebnis ist negativ, dann hat man eine Verstärkung.
Relativer Pegel
Der relative Spannungspegel ist der Unterschied zwischen 2 absoluten Spannungspegeln, und gibt das Verhältnis zweier Spannungen an.
 |
in dB | Leistungsdämpfung Leistungsverstärkung |
|---|
Leistung kann man in Spannung und Strom umrechnen.
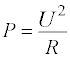
![]()
Wenn Eingangs- und Ausgangsleistung am gleichen Widerstand auftreten, dann kann der Widerstand herausgestrichen werden.
Damit die Spannungs- und Stromwerte nicht quadriert werden müssen wird der Multiplikator 10 (von Bel nach Dezibel) mit 2 multipliziert.
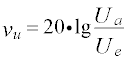 |
in dB | Spannungsdämpfung Spannungsverstärkung |
|---|---|---|
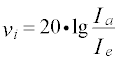 |
in dB | Stromdämpfung Stromverstärkung |
Wenn die Verstärkung einen negativen Wert hat, dann ist es eine Dämpfung.
In der Signaltechnik werden nur Leistungen und Spannungen über das logarithmische Verhältnis ausgerechnet und in Verstärkung/Dämpfung oder Pegel angegeben.
Absoluter Pegel

Setzt man den Bezugswert (Formelzeichen mit dem Index 0) auf einen definierten Wert, so wird aus dem relativen Pegel ein absoluter Pegel. Die dB-Angabe wird dann um eine Einheit erweitert. Zum Beispiel dBm oder dBµV. Diese Einheit gibt einen Wert bezogen auf den Bezugswert an. Da es sich um Wechselgrößen handelt wird immer mit Effektivwerten gerechnet und diese auch angegeben.
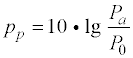
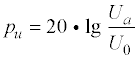
Beispiele
| Größe | Bezugswert | Einheit |
|---|---|---|
| Leistung P0 | 1 mW | dBm |
| Leistung P0 | 1 W | dBW |
| Spannung U0 | 1 µV | dBµV |
| Spannung U0 | 1 V | dBV |
| Spannung U0 | 774,6 mV | dBu |
| Strom I0 | 1 A | dBA |
| Strom I0 | 1,291 mA | dBi |
| Elektrische Feldstärke E | 1 µV/m | dB (µV/m) |
| Schallpegel SPL | 20 µPa | dB (A) |
Hinweis: Ein dB-Wert ist immer eine relative Größe. Dagegen ist z. B. ein dBm-Wert eine absolute Größe. In diesem Fall ist die absolute, gemessene Leistung relativ zu 1 mW angegeben.
Pegel und Leistung im Vergleich
| dBm | Watt |
|---|---|
| -140 | 0,01 fW |
| -130 | 0,1 fW |
| -100 | 100 fW |
| -70 | 100 pW |
| -60 | 1 nW |
| -50 | 10 nW |
| -40 | 100 nW |
| -30 | 1 µW |
| -20 | 10 µW |
| -10 | 100 µW |
| 0 | 1 mW |
| +10 | 10 mW |
| +20 | 100 mW |
| +30 | 1 W |
| +40 | 10 W |
| +50 | 100 W |
Pegelwerte und die zugehörigen Spannungs- und Leistungsverhältniss
| Pegel | Leistungsverhältnis | Spannungsverhältnis | Pegel | Leistungsverhältnis | Spannungsverhältnis |
|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1,258925412 | 1,122018454 | -1 | 0,794328235 | 0,891250938 |
| 2 | 1,584893192 | 1,258925412 | -2 | 0,630957344 | 0,794328235 |
| 3 | 1,995262315 | 1,412537545 | -3 | 0,501187234 | 0,707945784 |
| 4 | 2,511886432 | 1,584893192 | -4 | 0,398107171 | 0,630957344 |
| 5 | 3,16227766 | 1,77827941 | -5 | 0,316227766 | 0,562341325 |
| 6 | 3,981071706 | 1,995262315 | -6 | 0,251188643 | 0,501187234 |
| 7 | 5,011872336 | 2,238721139 | -7 | 0,199526231 | 0,446683592 |
| 8 | 6,309573445 | 2,511886432 | -8 | 0,158489319 | 0,398107171 |
| 9 | 7,943282347 | 2,818382931 | -9 | 0,125892541 | 0,354813389 |
| 10 | 10 | 3,16227766 | -10 | 0,1 | 0,316227766 |
| 15 | 31,6227766 | 5,623413252 | -15 | 0,031622777 | 0,177827941 |
| 20 | 100 | 10 | -20 | 0,01 | 0,1 |
| 30 | 1 000 | 31,6227766 | -30 | 0,001 | 0,031622777 |
| 40 | 10 000 | 100 | -40 | 0,0001 | 0,01 |
| 50 | 100 000 | 316,227766 | -50 | 0,00001 | 0,003162278 |
| 60 | 1 000 000 | 1 000 | -60 | 0,000001 | 0,001 |
| 70 | 1 * 107 | 3162,27766 | -70 | 1 * 10-7 | 0,000316228 |
| 80 | 1 * 108 | 10 000 | -80 | 1 * 10-8 | 0,0001 |
| 90 | 1 * 109 | 31 622,7766 | -90 | 1 * 10-9 | 3,16228 * 10-5 |
| 100 | 1 * 1010 | 100 000 | -100 | 1 * 10-10 | 0,000 01 |
| 120 | 1 * 1012 | 1 000 000 | -120 | 1 * 10-12 | 0,000 001 |
Weitere verwandte Themen:
Frag Elektronik-Kompendium.de
Elektronik-Fibel
Elektronik einfach und leicht verständlich
Die Elektronik-Fibel ist ein Buch über die Grundlagen der Elektronik, Bauelemente, Schaltungstechnik und Digitaltechnik.
Elektronik-Set Starter Edition
Elektronik erleben mit dem Elektronik-Set Starter Edition
Perfekt für Einsteiger und Wiedereinsteiger
- Elektronik-Einstieg ohne Vorkenntnisse
- Schnelles Verständnis für Bauteile und Schaltsymbole
- Ohne Lötkolben experimentieren: Bauteile einfach stecken
Keine Lust alleine zu experimentieren?
Dann buche einen Online-Workshop Elektronik Starter zum Elektronik-Set dazu. Unsere Online-Workshops sind praxisorientiert und bietet eine grundlegende und fundierte Einarbeitung in die Elektronik.
Elektronik-Fibel
Elektronik einfach und leicht verständlich
Die Elektronik-Fibel ist ein Buch über die Grundlagen der Elektronik, Bauelemente, Schaltungstechnik und Digitaltechnik.


